Fairy endgames

part of "Between chessboard and computer", Vaclav Kotesovec, 1996

Grashüpfer-Endspiele (cvrčkové koncovky)

Im folgenden Artikel sammelte ich die Ergebnisse meiner Forschungen auf diesem Märchenschachgebiet. Ich glaube, dass mein Artikel zur Entfaltung der Endspieltheorie und zur Entstehung vieler Märchenschachstudien beiträgt.

A) Mattführung mit 4 Grashüpfern

Ein Matt mit zwei Grashüpfern existiert überhaupt nicht; mit drei Grashüpfern gibt es zwar Matts, aber es ist unmöglich, sie zu erzwingen (Diagramm 1a/b). Aber mit vier GG und K ist der Gewinn zu bewältigen. Die Mattführung läuft in 3 Phasen ab:

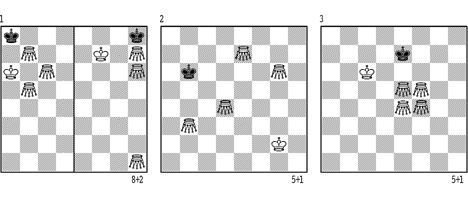
Die zwei ersten Phasen sind nicht schwierig. Schwarz kann nicht verhindern, dass Weiss ein GG-Quadrat aufbaut. In der Diagrammstellung 2 spielt Weiss z.B. so: 1.Kf3 Kc5 2.Ke3 Kd6 3.Ge2 Ke5 4.Kd3 Kf5 5.Ge4 Ke6 6.Ge1 Kd5 7.Ge3 Ke5 8.Gc4 Kd6 9.Gc3 nebst 10.Gb4, oder 7. - Kc6 8.Gc4 Kb5 9.Kc3 Kc6 10.Gd3 nebst 11.Ge4, oder 4. - Kf6 5.Gc2 Ke5 6.Gb2 Kd5 7.Ga1 und 8.Gc3, und das Quadrat ist fertig.

Für die zweite Phase sind die beiden folgenden Positionen charakteristisch. In der Stellung 3 spielt Weiss 1.Kc7 und nach 1. - Kf7 2.Kd7 Kg7 (2. - Kf8 3.Gf6 Kg8 4.Gg6) 3.Ke7 Kh6 4.Ge3 Kh5 5.Kf6 Kh4 6.Gf3 Kh5 7.Kg7 usw. ; oder 5. - Kh6 6.Kf7 Kh5 7.Kg7 Kh4 8.Gf3 Kh5 9.Kh7. Auf das bessere 1. - Ke8 antwortet Weiss: 2.Kd6 Kd8 (2. - Kf8 3.Gf6 Ke8 4.Ge6 usw.) 3.Ge6 Ke8 4.Gf6 Kd8 5.Kc6 Kc8 6.Kb6 Kd8 7.Kb7 oder 6. - Kb8 7.Gd7 usw.; analog nach 3. - Kc8 4.Kc6 Kb8 5.Kb6 Kc8 6.Gf6 usw.

In der Diagrammstellung 4 muss Weiss eine Zugzwangsituation schaffen. Er spielt darum 1.Kd5 Kg1 2.Ke5! (auf die verkehrte Seite; 2. - Kh2 3.Gf2 usw.) Kf1 3.Kd4 Kg1 4.Gg3 Kf1 5.Kd3 Ke1 6.Ge3 Kd1 7.Kc3 Kc1 8.Kb3 Kb1 9.Gd2 (8. - Kd1 9.Kb2). Andere Züge sind nicht besser, z.B. 1. - Kh3 2.Ke5 Kh4 3.Kf6 usw.

In allen Varianten der Stellungen 3 und 4 entstanden Positionen, die der Diagrammstellung 5 analog sind. Die dritte Phase verläuft hier so: 1.Ge8 Kg8 2.Kg6 Kh8 (Jetzt wird Weiss ein Tempo-Manöver machen:) 3.Gg7 Kg8 4.Gg5 Kh8 5.Ge7 Kg8 6.Gd6 Kh8 7.Gg7#. Die andere Variante: 1. - Kh7 2.Gd8 Kh8! 3.Kh6! Kg8 4.Kg6 Kh8 5.Gf6 Kg8 6.Gd8 Kh8 7.Gg7#.

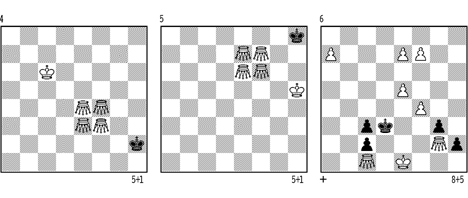
Zur Abwechslung führe ich meine Studie an (Diagramm 6). Schwarz droht 1. - h1D+, darum muss Weiss drei GG-Umwandlungen machen. Lös.: 1.a8G Ke4 2.e8G+ Kf3 3.f8G+ K:g2 4.Gh1! K:h1 5.Kf1 g2+ 6.Ke2 Kg1 7.Gg8+ Kh1 8.Gf3/Gh8#; 4. - Kg1 5.Ke2 g2 (5. - Kg2 6.d6 usw.) 6.Gf1+ Kh1 7.Gh3+ Kg1 8.Gg5/Gg8#; 3. - K:f4 4.Gh1 K:e5 5.Ke2 (4. und 5.Zug = austauschbar) Ke6 6.Ke3 Ke7 7.Gd6! und Weiss gewinnt.

B) Mattführung mit GG und leichten Figuren

Diagramm 7 a/b zeigt Matts mit G und S bzw. L, welches aber nicht zu erzwingen ist. Mit 2 GG und einer leichten Figur kann Weiss aber schon den sK mattsetzen.

1) Mattführung mit L und 2 GG

2) Mattführung mit S und 2 GG

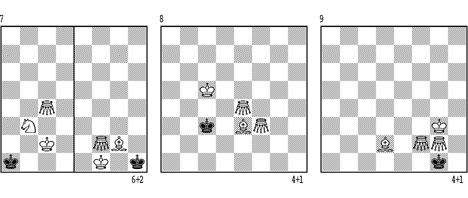
Diese Mattführung ist sehr langsam, sie kann mehr als 50 Züge dauern. Zuerst wird in 10 ein System gezeigt, wie Weiss den sK in die Ecke drängt. 1.Kc4 Ka3 (1. - Ka5? 2.Kb3 Ka6 3.Kb4 usw.) 2.Gc3 Ka2 3.Sb5 Kb1 4.Kd3 Kc1 (4. - Ka1/2 4.Kc2) 5.Sa3 Kd1 6.Gd2 Kc1 7.Sc2+ Kd1 (7. - Kb1 8.Ge3 Ka2 9.Kc3 Kb1 10.Sb4 Ka1 11.Kb3) 8.Se3 Kc1 9.Gd4 Kb1 10.Sc2 Ka2 11.Kc4 Kb1 12.Se3 Kc1! (nach 12. - Ka1 13.Kb3 Kb1 14.Gf3 Kc1 15.Kc3 Kb1 16.Sd1 und 17.Sb2; nach 12. - Ka2 13.Kb4 Kb1 14.Gf3 Kb2 15.Gd3 Kc1 16.Kc3 usw.) 13.Gb4 Kb1! (13. - Kb2 14.Gc5 Kc1 15.Kc3) 14.Kb3 Kc1 15.Ka3! Kb1 16.Gd2 Kc1 17.Gf4 Kb1 18.Kb3 Kc1 19.Gf3 Kb1 20.Kc3 Kc1 (20. - Ka2 21.Sc4 Kb1 22.Kd2) 21.Gd2 Kb1 22.Gd3 Kc1 23.Sc4 Kb1 24.Sb2 Kc1 (24. - Ka1 25.Kc2 Ka2 26.Sc4) 25.Ga2 Kb1 26.Gc2+ Kc1 27.Gc4 Kb1 (= Diagramm 11). Wenn Schwarz 2. - Ka4 spielt, dann 3.Sb7 Ka3 4.Sc5 Ka2 5.Sd3 Ka3 6.Sc1 Ka4 7.Gb4 und symmetrisch wie in der Hauptvariante.

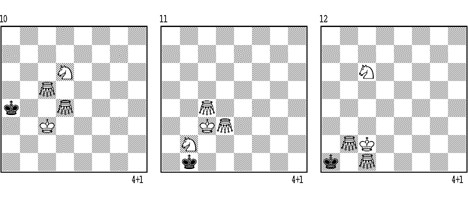
Wenn dem Weissen in der Schlussstellung ein Tempo fehlt, spielt er so (Diagramm 12): 1.Se5 Ka2 2.Sd3 Ka1 3.Kc3 Ka2! 4.Kb4 Ka1! 5.Ka3! Kb1 6.Kb3 Ka1 7.Ga3 usw.

3) Mattführung mit G und 2 SS

Sie ist sehr einfach. In der Diagrammstellung 13 gibt es zwei Möglichkeiten: 1.Gd5 Kh8 2.Sf8 Kg8 3.Sd7 Kh8 4.Sd6 Kg8 5.Sf7#, oder 1.Gf4 Kh8 2.Gf6 Kg8 3.Se7+ Kh8 4.Sg7#. Die Mattbilder sind analog denen der Stellungen 7a bzw. 11.

C) Endspiele: Drei Grashüpfer gegen Bauer

Hier liegt eine ähnliche Situation vor wie in Endspielen 2 wSS gegen sB. Das Matt kann nur erzwungen werden (bis auf einige Ausnahmesituationen – Diagramm 15), wenn der sB auf b6, b7 oder c7 (bzw. gespiegelt auf g6, g7, f7) steht. Dieser sB muss vom G blockiert werden, und der wK muss in der Nähe sein.

Für Weiss ist es am günstigsten, wenn der sB auf b6 (bzw.g6) steht. Dabei muss der zweite wG das Feld a6 (h6) decken. Diagramm 14 zeigt, wo der 3.wG stehen muss, damit Weiss gewinnen kann: er muss innerhalb der grossen Zone stehen (Anzug beliebig). Wenn wir einige triviale Felder (a5,a7,a8,c5) auslassen, existieren nur 4 “Remisfelder” (Vgl. Diagramm 14) b1, b2, g1 und h5. Weiss gewinnt, wenn sich der 3.wG ausserhalb der schraffierten Felder befindet.

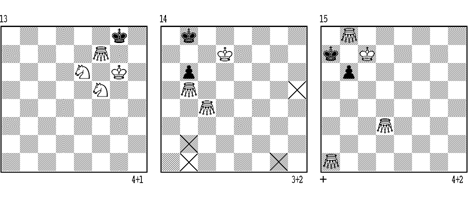
Diese Theorie möchte ich mit meiner “paradoxen” Studie (Diagramm 15) ergänzen. Wenn Weiss 1.Gb5? Ka8 2.Kd7 Ka7 3.Kd8 Kb8 4.Ga6 Ka8 5.Gc6 spielt, ist remis, denn 3. wG steht auf Remisfeld a1 (cooked, see following remark). Weiss kann diese Stellung aber trotzdem gewinnen: 1.Gd6! b5 2.Gd2 b4 3.Ga5 b3 4.Ga3 b2 5.Ga6+ Ka8 6.Gb7#. Auch nach anderen Antworten wird Schwarz in 6 Zügen matt, z.B. 1. - Ka8 2.Ga6 b5 3.Kc8 b4 4.Kc7 b3 5.Ga3 b2 6.Ga7#.

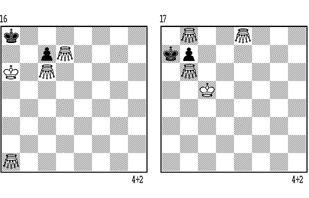
Steht der sB auf b7 oder c7 (bzw. g7, f7), so muss das Zusammenspiel der zwei übrigen GG gesichert sein, sonst ist die Partie remis. Z.B. in der Stellung 16 gewinnt Weiss so: 1.Gb7+ Kb8 2.Gd5 Ka8 3.Ga7 Kb8 4.Gd7 Ka8 5.Gb5 Kb8 6.Gb7# bzw. 6.Ge5+ Ka8 7.Gb7#.

Wenn Weiss das Matt bei der Position des sB auf b7 (bzw. g7) nicht erzwingen kann, ist es manchmal günstiger, den sB freizumachen und ihn zum Zug b7-b6 (g7-g6) zu zwingen. Dabei muss natürlich das Feld b5 (g5) von einem wG blockiert werden. In der Diagrammstellung 17 spielt Weiss darum so: 1.Gf8 Ka6 2.Gd8 Ka7 3.Gc8 Ka8 4.Kc4 Ka7 5.Kb5 Ka8 6.Ga5 Ka7 7.Kc5 Ka8 8.Gd5+ Ka7 9.Gb5 Ka8 10.Kd6 Ka7 11.Kc7 Ka8 12.Gd8! Ka7! 13.Gdb8 b6 14.Gd6 und gewinnt.

Exokoncovky (I)

Teorie exokoncovek je zajímavá přinejmenším ze dvou důvodů:

Zde se budu zabývat teorií cvrčkových koncovek a těším se, že tyto výsledky budou hojně používat skladatelé studií 21.století! Prvé kroky v teorii exokoncovek jsem učinil v článku “Grashüpfer-Endspiele”, který vyšel v časopise “feenschach” v roce 1977. Dokázal jsem, že proti samotnému králi vyhrávají: a) 4 cvrčci, b) střelec a 2 cvrčci, c) jezdec a 2 cvrčci, d) 2 jezdci a cvrček a dále jsem se zabýval koncovkou tří cvrčků proti pěšci.

Jako příklad jeden diagram ze zmíněného článku (schéma 1). Bílý vyhraje, stojí-li jeho třetí cvrček na některém z polí, kde je číslo. Stojí-li na polích b1, b2, g1 nebo h5, je remis. Ukažme si vyhrávající postup např. z pole e1. 1.Kd8 Ka7,8 2.Ke7 Kb8 3.Ce8 Kc8! 4.Ce6 Kc7 5.Cea6 Kc8 6.Cc6 Kb8 7.Kd8 Ka7,8 8.Kc8 Ka8 9.Cb7+ Ka7 10.Cc7#, (3. - Kc7 4.Ca4! Kc8 5.Cc6 a mat 9.tahem). Výhra je možná i z pole a1 (které bylo původně považováno za remízové) např. tímto postupem 1.Ca6 Ka8 2.Ke6 Kb8 3.Ke7 Ka8! (3. - Kc7 4.Ca7!) 4.Kf6 Kb8 5.Cg7 atd.

Dále je možná výhra v určitých postaveních bílých cvrčků při pozicích černého pěšce na c7 a b7, ale možnosti těchto koncovek jsou poměrně omezené. V dalším následují nové poznatky.

Tři cvrčci proti pěšci a3

Tato koncovka je velmi zajímavá a hledal jsem nějaké obecné pravidlo, jak rozhodnout, zda je vyhraná či remízová. Když vyloučíme postavení bílého cvrčka na a-sloupci, které je nezajímavé a není opodstatněné ani z retrográdního hlediska, je situace taková, že černý hrozí patem po a3-a2 a pokud bílý nemá k dispozici matovou hrozbu typu Cb1-Cc1, Cb2-Cc3 nebo mat skokem na a-sloupec, je pozice remízová. Taková je i většina náhodně vybraných pozic tří bílých cvrčků. Schémata 2-5 představují analýzu více než 200 pozic, které nás plně zasvětí do tajů této koncovky. Pozice vždy dvou bílých cvrčků jsou voleny pevně, třetí cvrček je na některém z volných polí. Je-li na tomto poli číslo, je pozice vyhraná v příslušném počtu tahů, jinak je pozice remízová.

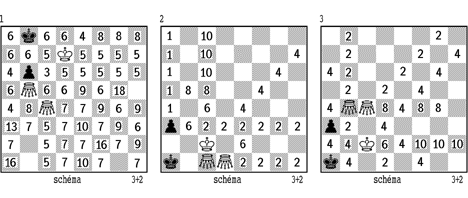
Největší hodnotu má schéma č.2. Ukažme si pro některé pozice vyhrávající postupy: Ch3 – 1.Kb3 a2 2.Ca3#; Ch1 – 1.Kb3 a2 2.Cb1#; Cc4 – 1.Cb1+ Ka2 2.Cd3 Ka1 3.Cc3 Ka2 4.Kc1 Ka1 5.Cb3 a2 6.Ca3#, 3. - a2 4.Kb3 Kb1 5.Cc2+ Ka1 6.Ca3#; Cc7 – 1.Cb1+ Ka2 2.Cc3 Ka1 3.Cc8 Ka2 4.Cc6 Ka1 5.Cc5 Ka2 6.Cc4 Ka1 7.Cc3 Ka2 8.Cd3 Ka1 9.Cb3 a2 10.Ca3#. K uvedeným analýzám je třeba poznamenat, že nejde o vícetažky, ale pouze o koncovky, jelikož postupy nejsou jednoznačné.

Řadu možností přináší i schéma 3. Např. při postavení třetího bílého cvrčka na f2, g2 nebo h2 vyhraje bílý takto: 1.Cd4 Ka2 (1. - a2? 2.Cb2#) 2.Ce4! Ka1 3.Cb2+ Ka2 4.Cd2 Ka1 5.Cc4 Ka2 6.Cd5 Ka1 7.Cb4 Ka2 (až sem je postup jednoznačný) 8.Kc1 nebo 8.Cb3 Ka1 9.Cb3(Kc1) a2 10.Ca4#.

Stojí-li bílý cvrček na g4, vzniká korektní osmitažka s řešením 1.Ch4 Ka2 (tahy černého krále nebudeme dále uvádět) 2.Ca4+ 3.Cd1 4.Ca4 5.Cc4 6.Cb3+ 7.Kc1 a2 8.Ca4#.

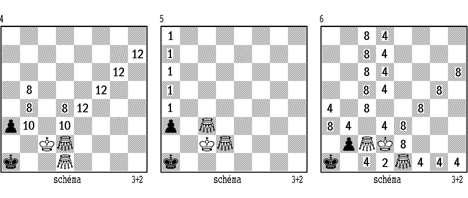
Rovněž v pozici 4 vzniká korektní osmitažka, stojí-li třetí bílý cvrček na poli d4. Řešení: 1.Cb3 2.Cd5 3.Cd3 4.Cb1 5.Cb4 6.Ca4 atd. je však trochu méně zajímavé. Ukažme si ještě postup z polí e4 až h7: 1.Cb1+ 2.Cbd3 3.Cb3 4.Cd4 5.Cb1 6.Cb4 7.Cb5 8.Ca4 9.Cc4 10.Cb3 11.Kc1 a2 12.Ca4#, který lze ovšem různě modifikovat.

Schéma 5 s sebou přináší základní pravidlo této koncovky: Při pozici cvrčků na c3 a d2 je pozice remízová, stojí-li třetí cvrček kdekoliv (s vyjímkou a-sloupce). Samozřejmě, že i některé vyhrané pozice lze převést nevhodným manévrováním bílými cvrčky na tuto pozici.

Tři cvrčci proti pěšci b2

Možnosti této koncovky ukazuje schéma 6. Pb2 nemůže táhnout a svou přítomností je černému spíše na obtíž. Ukažme si postup macení např.při pozici cvrčka na e2. 1.Kd3 Kb1 2.Cc4 Ka1 3.Kd2 Kb1 4.Cc1+ Ka1 5.Cf1 Kb1 6.Cd1 Ka1 7.Cc3+ Kb1 8.Cb3 nebo Cd3#. Postup je až na duál v matu jednoznačný.

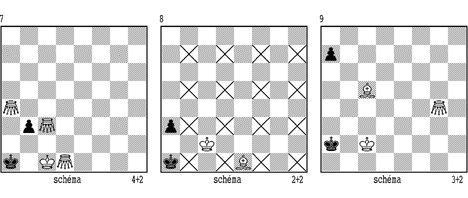
Na pozici s pěšcem b2 lze vyjímečně převést pozici s Pb3, jak ukazuje diagram 7: 1.Ca3 b2+ 2.Kd2 Kb1 3.Kc3 Ka1 4.Kb3 Kb1 5.Cc2 atd.

Střelec a cvrček proti pěšci

Jak plyne ze základní teorie, střelec a 2 cvrčci vyhrávají proti samotnému králi, pozice se střelcem a jedním cvrčkem je remízová. Má-li však černý pěšce, lze v některých případech jeho nevýhodnou pozici využít k výhře.

Schéma 8 s černým pěšcem a3 přináší tuto základní poučku: Stojí-li bílý cvrček na jednom z označených polí, je pozice remis při libovolné pozici bílého černopolného střelce.

Jinak bílý vyhraje (vyjímku tvoří pouze pozice Cd4-Sg1, Cg7-Sh8, Cc3-Sc1, je-li bílý na tahu). Příklad výhry si ukážeme se střelcem na e1 a cvrčkem např. na g5: 1.Sf2 Ka2 2.Se3 Ka1 3.Cd2 Ka2 4.Sc5 Ka1 5.Sb4 Ka2 6.Ca5+ Ka1 7.Se3#.

Na předcházející pozici lze převést pozice s černým pěšcem a4 až a7. Postup si ukážeme na diagramu 9: 1.Sd6 Ka1 2.Sa3 Ka2 3.Sb2 a6! 4.Sc1 Ka1 5.Sa3 Ka2 6.Sb2 a5 atd., až je pěšec donucen k tahu a4-a3.

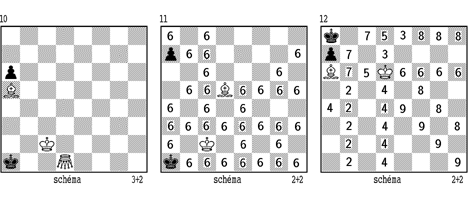
Diagram 8 nás seznámil s remízovými poli této koncovky, diagram 10 předvádí vyjímečnou možnost, kdy je bílý cvrček převeden na vyhrávající pole dříve než postoupí a-pěšec na a3. 1.Kb3! Kb1 2.Sd2 a5! 3.Ca4 Ka1 4.Kc2 Ka2 5.Sc1 Ka1 6.Ca6 Ka2 7.Sb2 a4 8.Sc1 Ka1 9.Se3 Ka2 10.Sb6 Ka1 11.Cc6 Ka2 12.Sc5 Ka1 13.Sa3 Ka2 14.Sb2 a3 15.Sc1 Ka1 16.Se3 Ka2 17.Sc5 Ka1 18.Sb6 atd.

Možnosti bělopolného střelce v podobné situaci ukazuje diagram 11. Ukažme si postup, je-li např. cvrček na a2: 1.Sc4 a6! 2.Kc1 a5 3.Ca6 a4 4.Cd3 a3 5.Sb3 a2 6.Ca3#, jedná se o korektní šestitažku.

Jiná možnost s bělopolným střelcem vzniká při pozici černého pěšce na a7, jak to ukazuje diagram 12. Např. při pozici cvrčka na h3 vzniká korektní osmitažka s řešením: 1.Kd7 Kb8 2.Cc8 Ka8 3.Kd8 4.Ce8 5.Kd7 6.Kc6 7.Cb5 Ka8 8.Sb7#. Je-li cvrček na b7, vzniká korektní sedmitažka, jejíž řešení přenechávám čtenářům.

Na doplnění uvádím (diagram 13) moji již publikovanou pětitažku (která má 2 řešení zakončená analogickými maty: 1.Sc7 a5 2.Sb8 a4 3.Ca5 a3 4.Kc7 a2 5.Cd8#, 1.Kc7 Ka7 2.Sb6+ Ka8 3.Sa7 a5 4.Kb6 a4 5.Sa5#.

Koncovka dvou stejnopolných střelců a cvrčka proti králi

Jak je jistě známo studiářům, dva stejnopolní střelci na výhru nestačí, přidáme-li však k nim ještě cvrčka, už ano. Obtížnost matového vedení lze srovnat s macením střelcem a jezdcem (matové vedení není odvozeno počítačem, takže je možné, že postupy lze zkrátit. Totéž platí i o výsledcích z předchozího článku.).

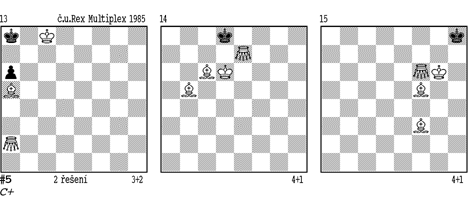
Je-li král v opačném rohu, postupujeme takto (diagram 15): 1.Ch6 Kg8 2.Kf6 Kh8(Kf8) 3.Sg6 Kg8 4.Sfe4 Kf8! (4. - Kh8 5.Sh7#) 5.Sef5 Kg8 6.Sh7+ Kf8 7.Ch8 Ke8 8.Sg8 Kd8 9.Ke6 Kc7 (9. - Ke8 10.Sg6+ Kd8 11.Kd6 atd.) 10.Kd5 Kb6 11.Sd7 Ka5 (11. - Kc7 12.Sb5 Kb6 13.Kc4 Ka5 14.Sf7 Kb6 15.Kb4 a jako dále) 12.Kc5 Ka6 13.Kb4 Kb6 14.Sb5 Kc7 15.Kc5 Kb7 16.Sf7 Kc7 17.Sc6 Kd8 (17. - Kb8 18.Kb6 Kc8 19.Sfe8 atd.) 18.Kd6 Kc8 19.Se8 Kb8 20.Kc5 Ka7 (20. - Kc7 21.Sd5 a 22.Kb6) 21.Kb5 Kb8 22.Kb6 Kc8 23.Scd7+ Kb8 24.Sf7 Ka8 25.Sfe6 Kb8 26.Sc8+ Ka8 27.Sd5#.

Exokoncovky (II)

Koncovka dvou obecných skokanů proti králi

Zatímco exoúlohami se dnes zabývá spousta skladatelů a počet originálů ve většině specializovaných časopisech převažuje nad počtem ortodoxních úloh, exostudie je vidět jen zřídka a těch, které využívají teoretických poznatků je ještě méně.

Důvodů k tomu je celá řada. Především styl skládání exostudií je v principu bližší studiím než exoúlohám, ale samotní studiáři si k nim zatím (celosvětově) nenašli cestu. Autory těch pár exostudií, které byly zatím publikovány, jsou vesměs úloháři.

Dalším důvodem malého výskytu exostudií je nedostatečně probádaná teorie exokoncovek. Tuto mezeru jsem se sám pokusil na některých místech vyplnit, zejména v oblasti cvrčkových koncovek.

Každý praktický šachista ví, že dva jezdci proti samotnému králi nestačí na vynucení matu. Již od mládí mně vrtala hlavou myšlenka, zda existují jiní dva obecní skokani (x1, y1) a (x2,y2) se kterými lze s pomocí vlastního krále zmatit z obecné pozice samotného soupeřova krále. Teprve éra osobních počítačů a zejména zvětšení kapacity jejich paměti mi umožnila vytvořit program, který dává plnou odpověď na tuto otázku.

Pro čtenáře méně zběhlé v terminologii exokamenů uvádím nejprve běžné značení nejznámějších bodových exokamenů, z nichž některé kameny pocházejí ještě z dávné šachové historie:

(0,1)=vezír (1,2)=jezdec (2,2)=alfil (0,2)=dababa (1,3)=velbloud (2,3)=zebra (1,1)=fers (1,4)=žirafa (3,4)=antilopa

Pro ostatní bodové kameny se používá obvykle označení např. (0,4)-skokan.

Následující tabulka přináší kompletní analýzu koncovek na šachovnicích 4x4, 5x5, 6x6, 7x7 a 8x8.

V případě vyhraných koncovek se uvažuje obecná pozice. Vyhratelné nejsou pozice ilegální (např.pro skokana (1,6) není legální pozice na d4) a pozice, kdy soupeřův král může přímo získat bílého skokana (např.bJa1,čKb2 a nekrytá pole c2,b3). Právě v boji o figuru existují některé zajímavé poziční remízy, které mohou být námětem pro exostudie, (např. Kd4 Jh7 velbloud Xh8 - Kf7, 1.Jg5 Kg7! 2.Xe7 Kf6! 3.Xh8 Kg7! 7.Xe7 Kf6 remis).

Tabulka koncovky dvou skokanů proti samotnému králi

Král + (x1,y1)skokan + (x2,y2)skokan – Král, 0 <= x1,x2,y1,y2 <= 7

Vyhrávající materiál podle velikosti šachovnice, kombinace kamenů a počtu tahů, v nichž lze vynutit mat.

                   4x4      5x5      6x6      7x7      8x8
 (0,1) + (0,2)     31        .        .       45y       .  
 (0,1) + (1,1)     15       18c      45       38c       .  
 (0,1) + (1,2)     17       22       29       38       45  
 (0,1) + (1,3)     20       30c      40       40c      77  
 (0,1) + (1,4)      .       38       37       45       55  
 (0,1) + (1,5)      .        .        .       50c       .  
 (0,1) + (1,6)      .        .        .       87       93  
 (0,1) + (2,4)      .       23c      65       43y       .  
 (0,2) + (1,2)      .        .       55       45y       .  
 (0,2) + (1,3)      .        .        .       44by      .  
 (1,1) + (1,2)     17       19c      36       37c       .  
 (1,1) + (2,3)      .        .        .       47c       .  
 (1,2) + (1,3)     21       21c      33       31c      49  
 (1,2) + (1,4)      .       37       34       36       41  
 (1,2) + (1,5)      .        .        .       36c       .  
 (1,2) + (1,6)      .        .        .       48       53  
 (1,2) + (2,4)      .       26c      60       33y       .  
 (1,3) + (2,4)      .        .        .       35by      .  

Speciálně – nejde vynutit mat dvěma skokany stejných hodnot.

Tyto výsledky jsou netriviální a bez pomoci počítače asi nezjistitelné. Uvědomíme-li si, že např. vynucení matu s materiálem vezír + (1,6)-skokan může v nejhorším případě vyžadovat až 93 tahů a dále skutečnost, že i silní praktičtí hráči mívají problémy s vynucením matu střelcem + jezdcem (což je proti tomu jednoduchá koncovka), je evidentní, že správně dokáže hrát asi jen počítač (hrací program, který matí krále s tímto materiálem jsem též vytvořil).

Následují příklady optimálního matového vedení při nejlepších obranách černého (samozřejmě jako vícetažky tyto pozice pro duály neobstojí).

V první fázi je nutné dostat oba bílé skokany pod kontrolu bílého krále: 1.Jc7! Kf2 2.Je8! Kg2 3.Wh4! Kg3 4.Wh5! Kg4 5.Jg7! Kf4 6.Kd3! Ke5 7.Je8! Kf5 8.Wh6! Kg5 9.Wh7! Kf5! 10.Ke3! Kg6 11.Wg7! Kf5 12.Kd4! Ke6 13.Kc5! Ke7 14.Jd6! Kf6 15.Wf7! Ke6 16.Kc6! Ke5 17.We7! Kf6 18.Jc8! Ke5 (nyní může začít zatlačování černého krále do rohu šachovnice) 19.Kc5! Ke4 20.We6! Kf5 21.Kd5! Kf4 22.Kd4! Kf5 23.We5! Kf6 24.Jd6! Ke7 (až sem byl postup jednoznačný) 25.Kd5 Kf6 26.Je4! Ke7 27.We6! Kf7 28.Ke5! Kg6 29.Wf6! Kh5 30.Kf5 Kh4 31.Wg6! Kh3 32.Kf4 Kg2 33.Wg5 Kf1 34.Ke3! Ke1 35.Jc3! Kf1 36.Wg4! Kg2 37.Ke2 Kh3 38.Kf3! Kh2 39.Wg3! Kg1 40.Ke2! Kh2 41.Kf2! Kh1 42.Je4 Kh2 (vynucení matu už je snadné) 43.Kf1! Kh1 44.Jf2! Kh2 45.Wh3# (nebo Wg2#).

1.Wg6 Kf5 2.Wg7 Kf6 3.Wg8 Kf7 4.Wh8 Kg6 5.Xe7 Kf6 6.Xf4 Kf5 7.Xc5 Kg6 8.Xd8 Kf6 9.Ka2 Ke7 10.Xc5 Kd6 11.Xb8 Kc7 12.Xa5 Kb6 13.Xb2 Kc6 14.Kb3 Kd5 15.Xe3 Kd4 16.Xh4 Kd3 17.Wh7 Kd4 18.Kb4 Kd5 19.Kc3 Kc5 20.Kd3 Kd5 21.Wg7 Kc5 22.Ke4 Kb4 23.Kd4 Kb5 24.Wg6 Kc6 25.Wf6 Kd6 26.Xg7 Kc6 27.We6 Kd7 28.Ke5 Kc6 29.Wd6 Kb5 30.Kd4 Kb6 31.Kd5 Kc7 32.Kc5 Kb7 33.Wd7 Kc8 34.Kc6 Kb8 35.Wd8 Ka7 36.Wc8 Ka6 37.Xf4 Ka7 38.Xe7 Ka6 39.Wb8 Ka7 40.Kc5 Ka6 41.Kd5 Ka5 42.Wb7 Ka6 43.Kc6 Ka5 44.Xf4 Kb4 45.Kd5 Kb5 46.Xg1 Ka5 47.Kc5 Ka6 48.Kc6 Ka5 49.Wb6 Kb4 50.Kd5 Kc3 51.Ke4 Kb4 52.Kd4 Ka5 53.Kc5 Ka4 54.Xf4 Kb3 55.Kd4 Kc2 56.Ke3 Kb3 57.Kd3 Kb4 58.Kd4 Kb3 59.Wb5 Kc2 60.Ke3 Kd1 61.Kd3 Kc1 62.Wb4 Kd1 63.Wb3 Kc1 64.Ke2 Kc2 65.Wb4 Kc1 66.Xe7 Kc2 67.Xd4 Kc3 68.Xc1 Kb2 69.Kd2 Ka2 70.Kc2 Ka1 71.Wb3 Ka2 72.Kc3 Ka1 73.Kd2 Ka2 74.Kc2 Ka1 75.Xb4 Ka2 76.Kc3 Kb1 77.Wb2#.

1.Wh2 Kf2 2.Wh3 Kg2 3.Wh4 Kg3 4.Wh5 Kg4 5.Wh6 Kg5 6.Wh7 Kf4 7.Gd8 Ke3 8.Ka2 Kd2 9.Ka3 Kc3 10.Wh6 Kd2 11.Kb4 Ke3 12.Kc5 Kf4 13.Gc4 Ke4 14.Kd6 Kd4 15.Gg5 Ke4 16.Gc6 Kd4 17.Wg6 Kc4 18.Ke5 Kc5 19.Gg5 Kb4 20.Kd4 Kb3 21.Wf6 Kb4 22.Wf5 Ka4 23.Kc4 Ka5 24.Wf6 Kb6 25.Wf7 Kc7 26.Kc5 Kd7 27.Kd5 Kc7 28.We7 Kb6 29.Kc4 Ka5 30.Wd7 Ka4 31.Gf1 Ka5 32.Gb2 Ka4 33.Wd6 Ka3 34.Ga6 Ka4 35.Wc6 Ka5 36.Gb2 Ka4 37.Wc5 Ka3 38.Ga6 Ka2 39.Kc3 Ka1 40.Kc2 Ka2 41.Wc4 Ka3 42.Ge5 Ka2 43.Wc3 Ka3 44.Wb3 Ka2 45.Gd1 Ka1 46.Gc5 Ka2 47.Kc3 Ka1 48.Kd2 Ka2 49.Kc2 Ka1 50.Gb1 Ka2 51.Ga5 Ka1 52.Ge4 Ka2 53.Ga3 Ka1 54.Ge2 Ka2 55.Wb2#.

1.Wg5 Kh4 2.Wg6 Kh5 3.Wg7 Kh6 4.Wf7 Kg6 5.We7 Kf6 6.Wd7 Ke6 7.Wc7 Kd6 8.Wb7 Kc6 9.Wa7 Kb6 10.Wa8 Kb7 11.Yb2 Kc6 12.Kc3 Kc5 13.Yh1 Kd5 14.Kb4 Kc6 15.Yg7 Kd5 16.Wa7 Kd4 17.Wa6 Kd3 18.Kc5 Kc3 19.Wa5 Kb3 20.Wb5 Kc3 21.Yf1 Kc2 22.Kc4 Kd2 23.Ye7 Kc2 24.Kd4 Kd2 25.Wc5 Ke2 26.Wd5 Kd2 27.We5 Kc2 28.We4 Kd2 29.We3 Ke1 30.Kd3 Kf2 31.Yd1 Kg3 32.Ke4 Kg4 33.Wf3 Kg5 34.Wf4 Kf6 35.Kd5 Kg5 36.Ke5 Kh4 37.Yc7 Kg3 38.Yb1 Kg2 39.Ya7 Kf1 40.Kd4 Kf2 41.Kd3 Kg3 42.Ke4 Kh4 43.Kf5 Kg3 44.Yg8 Kg2 45.Kg4 Kf1 46.Kf3 Ke1 47.Ke3 Kd1 48.Kd3 Kc1 49.We4 Kb2 50.Yh2 Ka2 51.Kc3 Ka3 52.Kc4 Ka4 53.Kc5 Ka5 54.Wd4 Ka6 55.Wc4 Kb7 56.Kd6 Kc8 57.Yg8 Kb7 58.Wb4 Ka6 59.Yh2 Kb6 60.Yb1 Ka6 61.Kc6 Ka5 62.Kc5 Ka6 63.Wb5 Kb7 64.Wb6 Kc8 65.Kd6 Kd8 66.Ke6 Ke8 67.Wb7 Kf8 68.Kf6 Ke8 69.Wc7 Kd8 70.Ke6 Ke8 71.Wd7 Kf8 72.We7 Kg7 73.Kf5 Kh6 74.Yh2 Kg7 75.Yb3 Kh6 76.Wf7 Kh5 77.Wf6 Kh6 78.Wg6 Kh5 79.Wg5 Kh6 80.Kf6 Kh7 81.Wg6 Kg8 82.Ke7 Kh7 83.Kf7 Kh8 84.Yh4 Kh7 85.Kf6 Kh8 86.Ke6 Kg8 87.Ke7 Kh8 88.Kf8 Kh7 89.Kf7 Kh8 90.Yb5 Kh7 91.Yh6 Kh8 92.Yb7 Kh7 93.Wg7#.

1.Xd4 Kg7 2.Xe7 Kf6 3.Xf4 Ke5 4.Xc5 Kd4 5.Xd8 Kc3 6.Ka2 Kc2 7.Ka3 Kc3 8.Ka4 Kc2 9.Kb4 Kd3 10.Kc5 Ke4 11.Jg6 Kf5 12.Jf8 Ke4 13.Je6 Kd3 14.Kd5 Ke3 15.Xa7 Kd2 16.Xd6 Kc1 17.Jf4 Kc2 18.Kd4 Kd2 19.Xg5 Kd1 20.Kc3 Ke1 21.Kc2 Kf1 22.Kd1 Kg1 23.Ke1 Kh1 24.Ke2 Kg1 25.Xd4 Kh1 26.Kf2 Kh2 27.Kf1 Kh1 28.Jd3 Kh2 29.Xe1 Kg3 30.Je5 Kh3 31.Kf2 Kh4 32.Xd4 Kh3 33.Kg1 Kh4 34.Kg2 Kh5 35.Kg3 Kh6 36.Kg4 Kg7 37.Xc7 Kg8 38.Kg5 Kh7 39.Jf7 Kg7 40.Jh6 Kh7 41.Jf5 Kh8 42.Kg6 Kg8 43.Jg7 Kh8 44.Jh5 Kg8 45.Jf6 Kh8 46.Jh7 Kg8 47.Xd4 Kh8 48.Xg5 Kg8 49.Jf6# (mat v rohu barvy velblouda).

Ka1 Je1 žirafa Gc2 – Ke2

1.Jg2 Kf3 2.Jh4 Kg4 3.Jg6 Kf5 4.Jf8 Ke4 5.Ka2 Kd3 6.Kb3 Kd4 7.Kb4 Kd3 8.Gb6 Kd4 9.Jg6 Kd5 10.Kc3 Kc5 11.Gc2 Kd5 12.Kd3 Ke6 13.Ke4 Kf6 14.Je5 Ke6 15.Jg4 Kd7 16.Kd5 Ke7 17.Gb6 Kd7 18.Jf6 Ke7 19.Ke5 Kf8 20.Jd5 Kg7 21.Je7 Kh6 22.Kf5 Kg7 23.Jg6 Kh6 24.Jf4 Kg7 25.Ke6 Kf8 26.Kd7 Kg7 27.Ke7 Kg8 28.Je6 Kh7 29.Kf6 Kh6 30.Jg7 Kh7 31.Jf5 Kh8 32.Ke6 Kg8 33.Ke7 Kh8 34.Kf8 Kh7 35.Kf7 Kh8 36.Je7 Kh7 37.Jg8 Kh8 38.Ga2 Kh7 39.Ge3 Kh8 40.Gd7 Kh7 41.Jf6#.

1.Jf2 Kf3 2.Jh3 Kg3 3.Jg5 Kf4 4.Jh7 Ke3 5.Kb2 Kd2 6.Yd7 Kd3 7.Kb3 Kd4 8.Kb4 Kd3 9.Kc5 Ke4 10.Kc4 Ke3 11.Kd5 Kd3 12.Jf6 Kc3 13.Ke4 Kc4 14.Je8 Kb4 15.Kd4 Kb3 16.Jf6 Kc2 17.Jd5 Kd2 18.Jc3 Kc2 19.Ye1 Kb3 20.Jd5 Kc2 21.Ke3 Kd1 22.Yf7 Kc2 23.Ke2 Kb2 24.Kd3 Kb3 25.Yg1 Kb2 26.Yh7 Kb3 27.Yb6 Kb2 28.Je3 Kb3 29.Yh5 Ka4 30.Kc4 Ka3 31.Yb6 Ka4 32.Jf5 Ka3 33.Kc3 Ka4 34.Jd6 Ka3 35.Yh5 Ka2 36.Jc4 Kb1 37.Jb2 Ka1 38.Kb3 Kb1 39.Jd3 Ka1 40.Yb6 Kb1 41.Yh7 Ka1 42.Yg1 Kb1 43.Kc3 Ka1 44.Kb4 Kb1 45.Kb3 Ka1 46.Jc1 Kb1 47.Je2 Ka1 48.Yf7 Kb1 49.Ye1 Ka1 50.Yd7 Kb1 51.Yc1 Ka1 52.Yb7 Kb1 53.Jc3#.

Následující tabulka představuje analýzu počtu vyhraných pozic podle materiálu na šachovnici 8x8 (jsou vybrány jen kombinace materiálu, kde je více než 10000 vyhraných pozic). Nejprve je vždy uvedena kombinace materiálu, počet vyhraných pozic, v dalším sloupci je pak počet skokanů ve dvojici, kteří mohou táhnout jen po polích jedné barvy, dále procento vyhraných pozic, když jsou skokani na polích stejné barvy (údaj kolem 50% znamená, že na tom nezáleží), poslední sloupec představuje procento vyhraných pozic z legálních pozic.

01 + 02    69068 1 52%  0%  11 + 12   473060 1 48%  3%
01 + 11   189956 1 49%  1%  11 + 23   311040 1 45%  2%
01 + 12 10872016 0 49% 92%  11 + 24    13728 2  0%  0%
01 + 13 11887200 1 49% 99%  11 + 34   112872 1 49%  0%
01 + 14 12030132 0 49% 98%  12 + 13 11588444 1 49% 99%
01 + 15   145644 1 52%  1%  12 + 14 11739768 0 49% 99%
01 + 16  9178728 0 49% 99%  12 + 15   379564 1 49%  3%
01 + 17    45624 1 50%  0%  12 + 16  8962428 0 49% 99%
01 + 24    95872 1 52%  0%  12 + 17   131576 1 50%  2%
02 + 02    13088 2  0%  0%  12 + 24   222616 1 51%  1%
02 + 12   172676 1 51%  1%  13 + 24   105936 2  0%  0%
02 + 13    81008 2  0%  0%  14 + 24    70916 1 49%  0%
02 + 14    37164 1 52%  0%  15 + 24    29704 2  0%  0%
02 + 15    17808 2  0%  0%  16 + 24    40380 1 48%  0%
02 + 16    24152 1 49%  0%  23 + 24   102856 1 49%  0%
02 + 23    95808 1 48%  0%  24 + 24    83712 2  0%  0%
02 + 24    34896 2  0%  0%  24 + 25    57848 1 49%  0%
02 + 25    27652 1 48%  0%  24 + 34    67912 1 50%  0%
02 + 34    51396 1 49%  0%

Endgame king and two leapers against king

Moje výsledky publikované v tomto článku byly dále reprodukovány v “The British Chess Magazine” 8/1994 (str.438) v rubrice “Quotes and Queries”, kterou řídí Ken Whyld (tomu dodal materiál John Beasley).

No. 5213 – Václav Kotěšovec has defined fully a special corner of chess knowledge in the April issue of the Slovak composition magazine, Pat a Mat, edited by Formánek in Bratislava. He has analysed by computer the endgame king and two leapers against king.

“What,” you may ask, “is a leaper?” A knight is a leaper – the only one found in orthodox chess. A leaper moves between two squares that have a relationship but no fixed path between them. That is often defined by the number of squares sideways followed by the number forward, or one of the many symmetrical variations. Thus the knight’s move is 1,2.

Other leapers found in fairy chess are the dabbaba (0,2), the camel (1,3), the giraffe (1,4), and the zebra (2,3). Less obviously leapers, because they move to adjacent squares, are the wazir (0,1) and the fers (1,1), but they share the characteristic of being unable to lose a move (unlike those pieces that can vary the length of their move or else triangulate). It is general knowledge that two knights cannot win against a bare king, and Kotěšovec has proved that no two leapers of the same kind can force mate. Two different leapers can in some cases do so, and he gives the number of moves needed from the least favourable position.

They are (0,1)+(1,2) 45; (0,1)+(1,3) 77; (0,1)+(1,4) 55; (0,1)+(1,6) 93; (1,2)+(1,3) 49; (1,2)+(1,4) 41; (1,2)+(1,6) 53. He also gives the information for 4x4, 5x5, 6x6, and 7x7 boards. Anyone seeking further data should apply to me or to my problemist colleague, John Beasley, who drew the topic to my attention.

A few examples are given in full, and readers might like to see how a knight and a giraffe (1,4) can succeed where two knights would fail, beginning with the white king on al, knight on e1, giraffe on c2, and black king on e2. 1.Sg2 Kf3 2.Sh4+ Kg4 3.Sg6 Kf5 4.Sf8 Ke4 5.Ka2 Kd3 6.Kb3 Kd4 7.Kb4 Kd3 8.Gb6 Kd4 9.Sg6 Kd5 10.Kc3 Kc5 11.Gc2 Kd5 12.Kd3 Ke6 13.Ke4 Kf6 14.Se5 Ke6 15.Sg4 Kd7 16.Kd5 Ke7 17.Gb6 Kd7 18.Sf6 Ke7 19.Ke5 Kf8 20.Sd5 Kg7 21.Se7 Kh6 22.Kf5 Kg7 23.Sg6 Kh6 24.Sf4 Kg7 25.Ke6 Kf8 26.Kd7 Kg7 27.Ke7 Kg8 28.Se6 Kh7 29.Kf6 Kh6 30.Sg7 Kh7 31.Sf5 Kh8 32.Ke6 Kg8 33.Ke7 Kh8 34.Kf8 Kh7 35.Kf7 Kh8 36.Se7 Kh7 37.Sg8 Kh8 38.Ga2 Kh7 39.Ge3 Kh8 40.Gd7+ Kh7 41.Sf6 mate.

To be able to make the comparable mate with two knights one of them would have to occupy the same square as the white king. If you set up the position after Black’s 35th, it is easy to see also how white can lose a move if necessary (as it would be if the giraffe were on a white square). The giraffe is manoeuvred to c7 and then the white king can triangulate, e.g. Kf6-e6-f7, followed by Se7-g8 and the giraffe then is manoeuvred to reach the position after move 40 above.

Exokoncovky (III)

VKSACH umí analyzovat prakticky všechny koncovky typu Kxy-K, kde x,y jsou exokameny. Vybral jsem ten nejzajímavější materiál a v každé tabulce číslo znamená v kolika tazích je daná koncovka nejpozději vyhratelná a pomlčka znamená, že je remízová.

Koncovky [endgames] se 3 kameny na normální šachovnici (normal board 8x8)

Koncovky se 4 kameny na normální šachovnici (normal board 8x8)

Např. s materiálem král + jezdec + tátoš zmatí bílý samotného černého krále nejpozději v 27 tazích. Též zebra, antilopa nebo fers nestačí spolu s jezdcem na vynucení matu, s tátošem už ano. Velbloud, žirafa nebo vezír jsou v tomto smyslu pro praktický šach o něco silnější. Dále je vidět, že silné kameny střelec, tátoš a růže většinou vyhrávají ve spolupráci i s jinak slabšími kameny. Překvapivě dost silný je i lion. Některé výsledky jsou evidentní, např. pokud vyhrává střelec s jezdcem, bude vyhrávat určitě i střelec s tátošem nebo růží. Zajímavé je, že k výhře stačí i střelec s fersem (různopolní), ale pomocí dvou fersů již mat vynutit nelze. Cvrček je jako materiál pro praktický šach velmi slabý kámen, tátošový cvrček je ještě slabší, o to kurióznější je, že tátošový cvrček spolu s růží stačí na výhru.

Koncovky se 3 kameny na válcové šachovnici (Zylinder 8x8)

Král s dámou zmatí samotného krále na válcové šachovnici nejpozději v 10 tazích, král s věží na zmacení soupeřova krále na válcové šachovnici nestačí, stejně tak nestačí střelec s jezdcem!

Koncovky se 4 kameny na válcové šachovnici (Zylinder 8x8)

Koncovky se 3 kameny na prstencové šachovnici (Ringzylinder 8x8)

Koncovky se 4 kameny na prstencové šachovnici (Ringzylinder 8x8)