Chess endgames with fairy pieces Pao, Vao, Leo, Lion and Grasshopper

Vaclav Kotesovec, 16.10.2002

see also previous article Cvrčkové koncovky po 25 letech (Grasshopper endgames after 25 years), Pat a Mat 38/2002 (p.206-208)
and old results Fairy endgames - part of "Between chessboard and computer", VK 1996

John Beasley created english version of both my articles for 'Variant Chess', issue 41:
Endings with Grasshoppers, Lions and Chinese pieces


V článku "Cvrčkové koncovky po 25 letech" jsem zmapoval pětikamenové koncovky se cvrčky (a ortodoxními kameny). Článek obsahoval základní informace včetně počítačového ověření dřívějších hypotéz.
Dále jsem se zabýval koncovkami s kameny Pao, Vao, Leo, Lion a zde publikuji nové výsledky. Teorie exokoncovek se tak rozrůstá a vzniká obrovský prostor pro skládání exostudií!

Summary: Minimal number of pieces of same value necessary for win in ending king and n same pieces against bare king are 4 GRASSHOPPERS, 3 LIONS, 2 LEOS or 3 PAOS


K+x+y-K     K+n*x-K
x / yCvrcekLionLeoPaoVaon
C(grasshopper)=    4
Lion==   3
Leo==+  2
Pao==+= 3
Vao==+==>4

První tabulka probírá 4-kamenové koncovky s možnými kombinacemi dvojic kamenů a v posledním sloupci pak minimální počet kamenů stejných hodnot, které spolu s králem stačí k výhře. Z kombinací dvou kamenů vyhrává pouze Leo+Pao, Leo+Vao a tím pádem i Leo+Leo, ostatní kombinace jsou remízové. Zajímavé je, že spolu s králem vyhrávají 4 cvrčkové, 3 Lioni, 2 Leové, 3 Paové, naopak ani 4 Vaové (bez ohledu barvy polí) na výhru nestačí.


Druhá tabulka probírá 5-kamenové koncovky s možnými kombinacemi trojic kamenů.

K+x+y+z-Kwin(+) / draw(=)
Pao+Pao+Pao+
Pao+Pao+Vao+
Pao+Vao+Vao+
Pao+Vao+Vao (stejnopolní)+
Vao+Vao+Vao=
  
C+C+C=
C+C+Lion+
C+Lion+Lion+
Lion+Lion+Lion+
  
C+C+Leo+
C+C+Pao+
C+C+Vao=


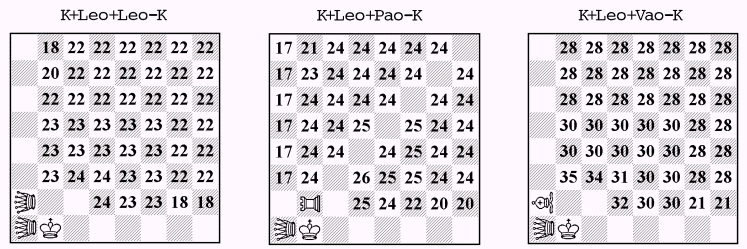
Následují diagramy se zafixovanými 4 (resp.3) kameny a počty tahů do matu při umístění pátého (resp.čtvrtého) kamene na některém z polí šachovnice. Ke každé koncovce uvádím příklad matového postupu (pro vybranou pozici jednu z možných variant)


Kb1 Leo a1a2 - Kc3, 1.Kc1 Kc4 2.Kd2 Kd4 3.LEOa1-d1+ Ke4 4.LEOa2-a5 Kf5 5.Ke3 Ke6 6.Kd4 Kf5 7.LEOd1-e2 Ke6 8.Kc5 Kd7 9.Kd5 Ke7 10.LEOe2-e5 Kd8 11.Ke6 Kc7 12.LEOe5-f6 Kd8 13.LEOa5-g5+ Kc7 14.LEOg5-h4 Kc8 15.Kd6 Kb7 16.LEOf6-e6 Kc8 17.LEOh4-h8 Kb7 18.LEOh8-h3 Ka8 19.Kc7 Ka7 20.Kc6 Ka8 21.Kb6 Kb8 22.LEOe6-d7 Ka8 23.LEOd7-e8 Kb8 24.LEOh3-h8#

Kb1 Leo a1 Pao b2 - Kd3, 1.Kc1 Ke3 2.Kc2 Ke4 3.Kc3 Ke5 4.Kc4+ Ke6 5.Kc5 Kf5 6.Kd5 Kf4 7.LEOa4 Kg5 8.Ke5 Kg4 9.PAOb3 Kg5 10.PAOb4 Kg6 11.LEOb5 Kf7 12.PAOc4 Ke8 13.Kd6 Kf8 14.PAOc6 Kf7 15.LEOb7 Ke8 16.Kc7 Kf8 17.Kd7 Kg8 18.Ke7 Kh8 19.Kf8 Kh7 20.LEOa6 Kh8 21.Kf7 Kh7 22.PAOd6 Kh8 23.Kg6 Kg8 24.LEOa3 Kh8 25.LEOa8 Kg8 26.PAOd8#

Kb1 Leo a1 Vao a2 - Kb3, 1.LEOb2 Ka3 2.VAOc4 Kb4 3.VAOf1 Kc3 4.Kc1 Kb3 5.LEOe5 Kc4 6.Kd2 Kd5 7.LEOh5 Ke4 8.LEOd1 Kf4 9.Kd3 Ke5 10.Ke3 Kd5 11.VAOe2 Ke6 12.Ke4 Kd6 13.LEOd2 Ke7 14.Ke5 Kd7 15.LEOd1 Kc6 16.Kd4 Kb5 17.Kc3 Kc6 18.VAOd3 Kc7 19.Kc4 Kc6 20.LEOd2 Kb7 21.Kb5 Kc7 22.Kc5 Kb7 23.LEOc3 Ka6 24.Kb4 Kb7 25.VAOc4 Kb6 26.LEOc2 Ka7 27.Ka5 Kb7 28.Kb5 Ka7 29.LEOb3 Ka8 30.Ka6 Kb8 31.LEOc2 Ka8 32.Kb6 Kb8 33.LEOc3 Ka8 34.LEOh8 Kb8 35.VAOg8#


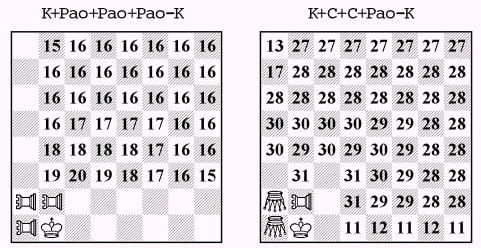
Kb1 Pao a1a2b2 - Kc3, 1.PAOb2-c2 Kb3 2.PAOc2-e2 Kc3 3.Kc1 Kd3 4.Kb2 Ke4 5.Kc2 Kf5 6.Kd3 Kf4 7.Kd4 Kf3 8.PAOe2-e5 Kg4 9.PAOa2-a5 Kf3 10.PAOa1-a3 Kf4 11.PAOe5-c5 Kg3 12.Ke3+ Kg4 13.PAOc5-d5 Kh4 14.Kf4 Kh3 15.Kf3+ Kh4 16.PAOa3-a4 Kh3 17.PAOd5-d4 Kh2 18.Kf2 Kh3 19.PAOa5-h5 Kh2 20.PAOd4-h4#

Kb1 Grasshopper a1a2 Pao b2 - Kd3, 1.Gc2 Kc4 2.Kc1 Kd4 3.Gd1 Kd3 4.Gb1+ Kc3 5.PAOb7 Kb4 6.Kd2 Kc5 7.Gd3 Kd6 8.PAOb1 Kd5 9.PAOe1 Ke6 10.Ge2+ Kf7 11.PAOd1 Ke6 12.Ke3 Kf5 13.Ge4+ Kg4 14.PAOc1 Kg5 15.Kf3 Kf6 16.PAOe1 Kg5 17.Kg3 Kf6 18.Kg4 Kg7 19.Gf5 Kf8 20.PAOe2 Kg8 21.PAOf2 Kg7 22.PAOf3 Kh6 23.PAOg3 Kh7 24.PAOg2 Kh8 25.Gh1 Kh7 26.Kg5 Kh8 27.Gh5 Kh7 28.Kf6 Kg8 29.PAOf2 Kh7 30.Kf7 Kh8 31.PAOh2#


Ka1 Pao b1b2 Vao a2 - Kc1, 1.PAOb2-b4 Kc2 2.PAOb4-g4 Kb3 3.PAOb1-h1 Ka4 4.PAOh1-h4+ Kb5 5.Kb2 Kc6 6.Kc3 Kd5 7.Kd2 Ke6 8.PAOg4-c4+ Kf5 9.Ke3 Kg4 10.Ke4+ Kg5 11.PAOc4-d4 Kf6 12.VAOd5 Kg5 13.PAOh4-f4 Kf6 14.PAOf4-f2 Kf7 15.Kf5+ Ke7 16.PAOd4-d3 Ke8 17.Ke6 Kf8 18.Kf6+ Ke8 19.PAOf2-e2 Kf8 20.PAOd3-e3 Kg8 21.Kg6 Kf8 22.VAOe6 Kg8 23.PAOe3-b3 Kf8 24.PAOb3-b8 Kg8 25.VAOc8#

Kb3 Pao a2 Vao b1b2 - Kd3, 1.Kb4 Kd4 2.PAOa4+ Ke5 3.Kc5 Ke4 4.VAOc3 Kd3 5.Kb4 Kc2 6.VAOa2 Kd3 7.VAOd5 Kc2 8.Kc4 Kd2 9.VAOd4 Kc2 10.PAOa3 Kd1 11.Kd3 Kc1 12.Kc3 Kd1 13.VAOb3 Kc1 14.PAOa2 Kd1 15.Kb2 Ke1 16.Kc2 Kf1 17.Kd2 Kg1 18.Ke2 Kh1 19.VAOd1 Kg1 20.Kf3 Kh2 21.PAOa3 Kg1 22.VAOc3 Kh2 23.Kf2 Kh1 24.Kg3 Kg1 25.PAOa1#

Kb1 Pao a2 Vao a1b2 - Ka4, 1.VAOb2-c3 Kb3 2.PAOb2 Kc4 3.Kc2 Kd4 4.PAOb3+ Ke4 5.Kd2 Kd5 6.Kd3 Ke6 7.Kc4 Kf5 8.VAOc3-d4 Kf4 9.VAOa1-c3 Ke4 10.Kc5 Kf5 11.Kd5 Kg4 12.Ke5 Kg5 13.PAOb4 Kg6 14.Ke6 Kg5 15.PAOc4 Kg6 16.VAOd4-e5 Kh5 17.VAOc3-d4 Kg5 18.PAOb4 Kh6 19.Kf5 Kh7 20.Kf6 Kg8 21.VAOd4-e3 Kh7 22.Kf7 Kh6 23.PAOb5 Kh7 24.VAOe5-f4 Kh8 25.VAOf4-h6 Kh7 26.PAOg5 Kh8 27.PAOh5#



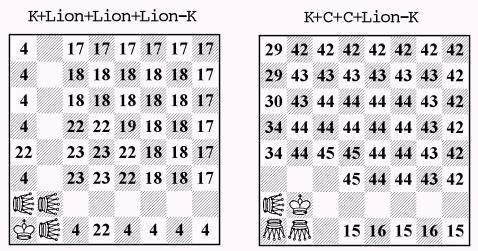
Ka1 Lion a2b1b2 - Kd3, 1.LIa2-g2 Kc3 2.Ka2 Kc2 3.LIb2-e2+ Kd3 4.LIe2-a6 Kc2 5.LIg2-b2 Kc3 6.LIa6-a1+ Kc4 7.Ka3 Kd3 8.Kb4 Kd2 9.Kb3 Ke3 10.Kc4 Kf4 11.LIa1-c3 Kg5 12.LIb1-b5 Kf4 13.LIc3-c5 Ke3 14.LIb2-b6+ Kf4 15.LIb6-b4+ Ke3 16.LIc5-c3 Kf3 17.LIb5-d3+ Ke2 18.LIb4-d4 Kf1 19.Kb3 Ke2 20.Kc2 Kf1 21.LId4-b2 Ke1 22.LIc3-a1 Kf1 23.LId3-b1#

Kb2 Grasshopper a1b1 Lion a2 - Kc4, 1.Gc3 Kd5 2.Kb3+ Kc6 3.Gb4 Kc5 4.Gb2 Kd6 5.Kc4 Ke5 6.Gd4+ Kd6 7.LId5+ Ke6 8.Gc5 Kd7 9.LIb3 Kc6 10.Gb4 Kd7 11.Kd5 Ke7 12.LIe6 Kf6 13.LIc4 Kg5 14.Gd4 Kf6 15.Ge5+ Kf5 16.Kd6 Kg6 17.Ke6 Kg5 18.Gc3 Kg6 19.Gc5 Kg5 20.Ge3 Kg6 21.LIf4 Kh5 22.Kf5 Kh4 23.Gg5 Kg3 24.LIf6 Kh2 25.Kf4 Kg1 26.Gg4 Kg2 27.Gg3+ Kg1 28.Kf3 Kh2 29.LIf2 Kh3 30.Kf4 Kh2 31.LIf5 Kh1 32.Ke3 Kg1 33.Kf3 Kh2 34.Kf2 Kh1 35.Ge6 Kh2 36.LId7 Kh1 37.LIg4 Kh2 38.Kf3 Kh1 39.Ke2 Kh2 40.Kf2 Kh1 41.Gh3 Kh2 42.Gf3 Kh1 43.LId1 Kh2 44.LIh5 Kh1 45.Gh3#