Lze stávajícími programy řešit úlohy například na šachovnici 4x4 ? Ano, ale zatímco WINCHLOE a VKSACH umožňují definovat velikost šachovnice, u programů ALYBADIX a POPEYE si musíme pomoci malým trikem, kdy zablokujeme zbytek šachovnice nebratelnými kameny bez možnosti tahu.
VKSACH - lze definovat velikost šachovnice v rozmezí 3x3 až 10x10. Bez problémů do velikosti 8x8 (Pro 9x9 a 10x10 bez možnosti zobrazení šachovnice, s omezením na "krátké skokany", x,y≤4, dále nelze použít redukční algoritmus ani některé jiné optimalizace). Příklad INP souboru pro úlohu na šachovnici 4x4 vypadá takto:
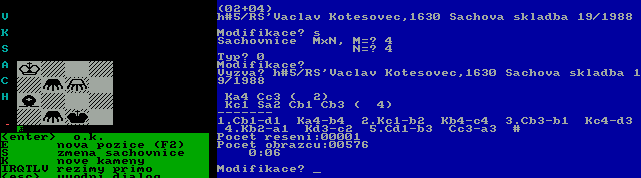
4 4 0 h#5/RS'Vaclav Kotesovec,1630 Sachova skladba 19/1988 Ka4Cc3 Kc1Sa2Cb1Cb3
WINCHLOE - lze definovat velikost šachovnice v rozmezí 1x1 až 250x250 zcela bez problémů
ALYBADIX - šachovnice je vždy 8x8. Pro menší šachovnice je jednou z možností umístit na ostatní pole kámen Pyramid. Pozor, nutné jsou obvykle minimálně 2 řady, protože přes tento kámen mohou skákat přeskakující kameny. Na druhé straně není nutné vždy zaplňovat šachovnici celou, protože to zbytečně zvětšuje rozměr položky v hashovacích tabulkách (což může citelně omezit maximální počet pozic zejména u úloh s málo kameny). Ovšem v případě přítomnosti delších skokanů musíme zablokovat více řad (pokud bude např.na šachovnici Zebra, budou nutné 3 řady). Vstup pro program AW (který vytvoří binární soubor typu POS pro Alybadix) bude vypadat takto:
problem: 001 notation: PJSVDKGN special: tree stipulation: h#5 title1: Vaclav Kotesovec title1: 1630 Sachova skladba 19/1988 white: Ka4 Grasshopper c3 black: Kc1 Sa2 Grasshopper b1b3 black: Pyramid a5a6b5b6c5c6d5d6e1e2e3e4e5e6f1f2f3f4f5f6 endproblem:A takto se zobrazí pozice v programu APwin

Jak mě informoval Ilkka Blom, vhodnějším kamenem je Edge-Block. V tom případě se totiž nehybné kameny neukládají do hashovacích tabulek (The non-moving/non-capturable pieces are eliminated during solving. Thus they do not take hash room!).
Navíc u pozic s maximálně 5 kameny (4 kameny ve verzi 2001) je vhodné vycentrování pozice doprostřed šachovnice. Pak se ušetří další paměť, protože program testuje symetrické pozice. Samozřejmě toto centrování je možné jen pro šachovnice 4x4 nebo 6x6, ale nelze použít pro liché rozměry (3x3, 5x5 nebo 7x7)
Zadání předchozí pozice by bylo následující:
white: Kc6 white: Edge-Block a1a2a3a4a5a6a7a8b1b2b3b4b5b6b7b8c1c2c7c8d1d2d7d8 white: Edge-Block e1e2e7e8f1f2f7f8g1g2g3g4g5g6g7g8h1h2h3h4h5h6h7h8 white: Grasshopper e5 black: Ke3 Sc4 Grasshopper d3d5V APwin vypadá pak takto:

Příklad jiné úlohy na šachovnici 4x4 se zasvěceným (anglickým) komentářem autora je též na konci stránky Alybadix solving examples
Poznámka: V obou případech nedoporučuji používat parametr sq-E (square edge), který definuje, že mat musí být na okraji šachovnice. Okraj šachovnice zůstává stále definován jako pro šachovnici 8x8, takže se může stát, že program v tomto případě nenajde řešení! Pozor na to, sám jsem na to při řešení narazil a chvíli nechápal proč program nenajde například mat 1.tahem - až mi to za chvíli došlo...
POPEYE - šachovnice je vždy 8x8. Pro menší šachovnice je nutno použít Loch (angl. Hole). Tento vstupní soubor lze vygenerovat také programem OUTPY z VKSACHového vstupu.
Anfangproblem Autor Vaclav Kotesovec Quelle 1630 Sachova skladba 19/1988 Forderung h#5 Steine Weiss Ka4 Gc3 Steine Schwarz Kc1 La2 Gb1 Gb3 bed Loch a5a6a7a8b5b6b7b8c5c6c7c8d5d6d7d8e1e2e3e4e5e6e7e8f1f2f3f4f5f6f7f8g1g2g3g4g5g6g7g8h1h2h3h4h5h6h7h8 Protokoll SMALL.LST EndeProblem
Obecně je nutné vyblokovat všechna nevyužitá pole šachovnice (například Zebra může přes jednořadový Loch přeskočit!) Cvrček ovšem přeskočit přes Loch nemůže, takže v tomto případě stačí jen
bed Loch a5b5c5d5e1e2e3e4e5
Popeye WINDOWS98-32Bit-Version 3.75 (2048 KB)
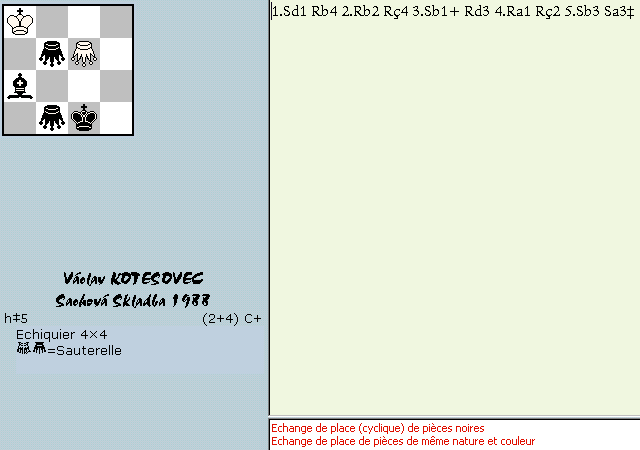
Vaclav Kotesovec
1630 Sachova skladba 19/1988
+---a---b---c---d---e---f---g---h---+
| |
8 . . . . . . . . 8
| |
7 . . . . . . . . 7
| |
6 . . . . . . . . 6
| |
5 . . . 5
| |
4 K . . . . . . 4
| |
3 . -G G . . . . 3
| |
2 -L . . . . . . 2
| |
1 . -G -K . . . . 1
| |
+---a---b---c---d---e---f---g---h---+
h#5 2 + 4
1.Gb1-d1 + Ka4-b4 2.Kc1-b2 Kb4-c4 3.Gb3-b1 + Kc4-d3 4.Kb2-a1 Kd3-c2 5.Gd1-b3 Gc3-a3 #
Loesung beendet. Zeit = 3.850 s