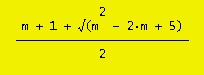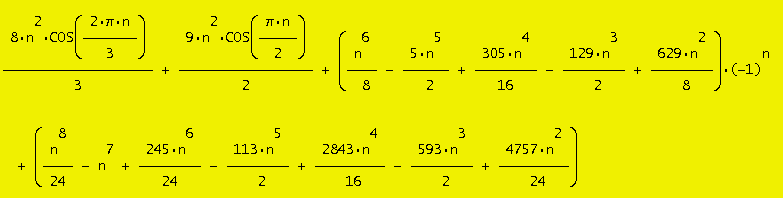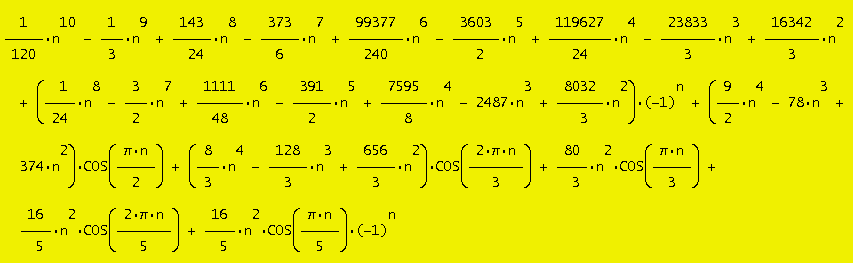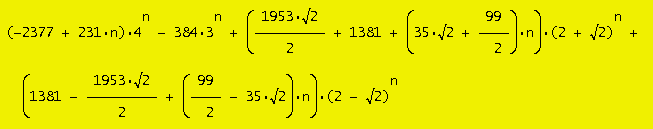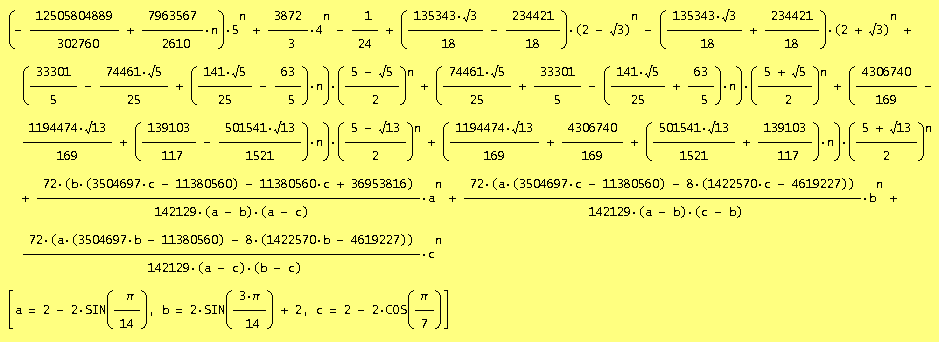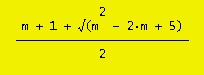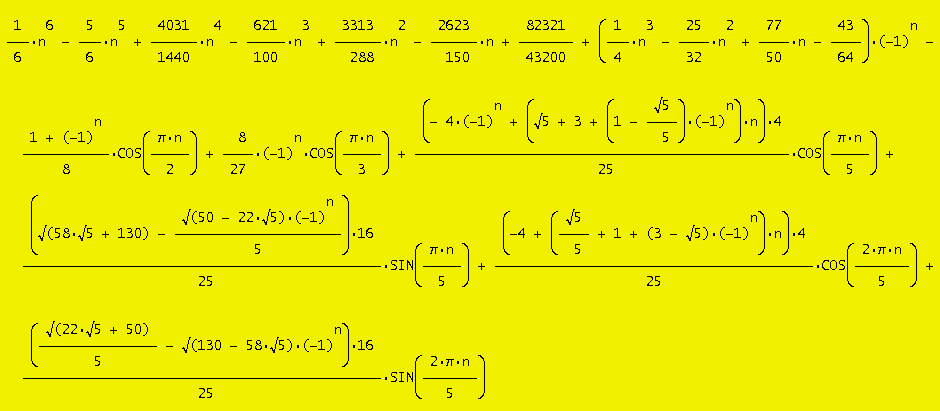Number of ways of placing non-attacking queens, kings, bishops and knights on boards of various sizes

OLD ARTICLE (no longer updated!)

For compatibility of links I keep this page, but I strongly recommend my book in PDF format with all these results and much more.
The book was published 22.4.2010, second edition 23.6.2010, third edition 19.1.2011, fourth edition 15.6.2011, fifth edition 9.1.2012, sixth edition 2.2.2013.

Number of ways of placing non-attacking
queens, kings, bishops and knights

on boards of various sizes

(Vaclav Kotesovec, 1996-2010)

This article is based on part of book "Between chessboard and computer", Vaclav Kotesovec, 1996. Pages 204-6 is a straight piece of combinatorial mathematics concerning the number of ways of placing non-attacking kings and queens on boards of various sizes. Now new results and formulas since 1996 are published.

Tento článek je věnován problematice počtu rozmístění neohrožujících se kamenů stejných hodnot na různých velikostech a typech šachovnic. Nejznámější z těchto problémů je tzv. n-Queens problem, který řeší počet rozmístění n neohrožujících se dam na šachovnici n x n. O tomto problému byla napsána již spousta článků a základní informace a přehled linků je možno nalézt na mojí stránce links. Můj článek má ale širší záběr a věnuje se různým typům kamenů i šachovnic. Základ článku tvoří jeho verze z roku 1996, publikovaná v mé knize "Mezi šachovnicí a počítačem", str.204-206. Od roku 1996 došlo k výraznému zrychlení počítačů, což umožnilo získat další výsledky a odvodit řadu nových vzorců.

Content - Obsah

1.1 Queens on board n x n
1.2 Queens on board k x n
1.3 Conjectures for Q(n), n ® Ą
1.4 Queens on toroidal board n x n

2.1 Kings on board n x n
2.2 Kings on board k x n
2.3 Kings on boards of various size

3.1 Rooks on board n x n
3.2 Rooks on board k x n

4.1 Bishops on board n x n
4.2 Bishops on board k x n

5.1 Knights on board n x n
5.2 Knights on board k x n
5.3 Knights on cylindrical board n x n
5.4 Knights on toroidal board n x n

6.1 Nightriders on board n x n
6.2 Nightriders on board k x n

7.1 Amazons (superqueens) on board n x n
7.2 Amazons (superqueens) on board k x n

8.1 Zebras on board n x n
8.2 Zebras on board k x n

9.1 Wazirs on board n x n
9.2 Wazirs on board k x n

10. Other fairy pieces

1.1) Queens on board n x n - Dámy na šachovnici n x n

2 Queens, board nxn (E.Lucas, 1891): n(n-1)(n-2)(3n-1)/6

3 Queens, board nxn (E.Landau, 1896): n(n-2)²(2n³-12n²+23n-10)/12, pro n sudé (even),
(n-1)(n-3)(2n⁴-12n³+25n²-14n+1)/12, pro n liché (odd)

4 Queens, board nxn (V.Kotesovec, 1992): n>=2 : n⁸/24 - 5n⁷/6 + 65n⁶/9 - 1051n⁵/30 + 817n⁴/8 - ...

a dále podle typu n:

a) n=6k, -4769n³/27 + 1963n²/12 - 1769n/30

b) n=6k+1, -9565n³/54 + 1013n²/6 - 6727n/90 + 257/27

c) n=6k+2, -4769n³/27 + 1963n²/12 - 5467n/90 + 28/27

d) n=6k+3, -9565n³/54 + 1013n²/6 - 2189n/30 + 7

e) n=6k+4, -4769n³/27 + 1963n²/12 - 5467n/90 + 68/27

f) n=6k+5, -9565n³/54 + 1013n²/6 - 6727n/90 + 217/27

Koeficienty u n³ a n², jdou vyjádřit také takto: -19103/108 + (-1)ⁿ/4 , -3989/24 - 21(-1)ⁿ/8

V roce 2005 našel S.Perepechko pro tento můj vzorec zápis formálně sjednocující všech 6 případů. Sergey Perepechko (2005) convert these 6 formulas by Vaclav Kotesovec (1992) into 1 unified expression, kde [x]=floor(x) je celá část (largest integer not greater than x)
n(n-1)(45n⁶-855n⁵+6945n⁴-30891n³+78864n²-106226n+53404)/1080 + (n³-21/2*n²+28n-14)[n/2]+32/9(n-1)[n/3]+(16/9*n-4)[(n+1)/3]

Na základě řešení diferenční rovnice jsem ještě odvodil jiný jednotný vzorec pro tuto funkci (dávající pro celočíselné hodnoty n stejné výsledky):
n⁸/24 - 5n⁷/6 + 65n⁶/9 - 1051n⁵/30 + 817n⁴/8 - 19103n³/108 + 3989n²/24 - 18131n/270 + 253/54 + (n³/4 - 21n²/8 + 7n - 7/2)*(-1)ⁿ + 32(n-1)/27*COS(2*pi*n/3) + 40/81*3^(1/2)*SIN(2*pi*n/3)

Pro k dam na šachovnici n x n je odhad průběhu této funkce:
n^2k/k!-5/3n^2k-1/(k-2)!+O(n^2k-2)

Důkaz, že pro libovolné k je příslušná vytvořující funkce (generating function) racionální (tedy že jde o podíl dvou polynomů s celočíselnými koeficienty) uvádí v knize "Enumerative Combinatorics", vol. I (1986), Richard P. Stanley (chapter 4, exercise 15, solution page 280-1). Tím je dán tvar řešení pro všechny tyto funkce, který obsahuje vždy polynom s konstantními koeficienty plus součet dalších tzv. Quasi-polynomů (nazývaných též "pseudo-polynomial" nebo "polynomial on residue classes"), což jsou polynomy, jejichž koeficienty jsou periodické funkce s integer periodou. Odtud vyplývá, že k nalezení příslušného vzorce pro danou sekvenci potřebujeme vždy znát jen dostatečný počet známých hodnot. Potom jde o nalezení nejmenší periody a určení koeficientů přílušných polynomů. Háček je jedině v tom, že časově možný je výpočet jen do určité hodnoty n a ta nemusí být postačující pro nalezení všech koeficientů (viz např. případ 3 tátošů, kde jsem pro objevení obecného vzorce potřeboval přes 300 hodnot!). Proto vzorce pro vyšší hodnoty k budou postupně přibývat až se zrychlováním počítačů.

Vzorce jsou i v On-Line Encyclopedia of Integer Sequences (Neil J. A. Sloane)
A036464 - 2Q NxN
A047659 - 3Q NxN
A061994 - 4Q NxN
A108792 - 5Q NxN - I found formula, see my book kotesovec_non_attacking_chess_pieces_2011_4ed.pdf for more!

Viz Edouard Lucas: Théorie des nombres (1891), vzorec pro počet rozmístění 2 neohrožujících se dam najdeme na str.98, dále je uveden též v knize Edouard Lucas: Récréations mathématiques (1894) str.132
Viz Naturwissenschaftliche wochenschrift (1896) - v čísle z 2.8.1896, str.367-371 (str.380 v PDF) je článek "Ueber das Achtdamenproblem und seine Verallgemeinerung", jehož autorem je Edmund Landau. V článku jsou odvozeny vzorce pro rozmístění 3 dam na šachovnici n x n (pro sudé a liché n). Je zajímavé, že tento slavný německý matematik objevil vzorec už ve svých 19 letech.

Této problematice byly věnovány také 2 články ve francouzském časopise "Rex Multiplex". Ve druhém byly publikovány moje nové výsledky.
Rex Multiplex 18/1986, (page 615, Louis Azemard, Echecs et Mathématiques) "Placements et Configurations pour 2, 3 et 4 Dames"
Rex Multiplex 38/1992, (Louis Azemard, Echecs et Mathématiques), "Une communication de Vaclav Kotesovec"

Poznámka: Panos Louridas publikoval v idee & form 93/2007 (str. 2936-2938) obecnější vzorec pro rozmístění 3 dam na šachovnici m x n. Vzorec je však dost neelegantní (zabírá skoro půl stránky), proto zájemce odkazuji na tento článek.

Tabulka udává rozmístění k dam na šachovnici nxn, diagonála odpovídá problému n-dam.

n	k=2	k=3	k=4	k=5	n queens, nxn
2	0				0
3	8	0			0
4	44	24	2		2
5	140	204	82	10	10
6	340	1024	982	248	4
7	700	3628	7002	4618	40
8	1288	10320	34568	46736	92
9	2184	25096	131248	310496	352
10	3480	54400	412596	1535440	724
11	5280	107880	1123832	6110256	2680
12	7700	199400	2739386	20609544	14200
13	10868	348020	6106214	60963094	73712
14	14924	579264	12654614	162323448	365596
15	20020	926324	24675650	396155466	2279184
16	26320	1431584	45704724	899046952	14772512
17	34000	2148048	80999104	1917743448	95815104
18	43248	3141120	138170148	3879011584	666090624
19	54264	4490256	227938788	7491080844	4968057848
20	67260	6291000	365106738	13892164232	39029188884
21	82460	8656860	569681574	24854703014	314666222712
22	100100	11721600	868289594	43071383040	2691008701644
23	120428	15641340	1295775946	72532831794	24233937684440
24	143704	20597104	1897176508	119038462248	227514171973736
25	170200	26797144	2729909796	190849299076	2207893435808352
26	200200	34479744	3866439956	299547508728	22317699616364044
27	234000	43915768	5397191260	461105824676	?
28	271908	55411720	7434046062	697264240408	?
29	314244	69312516	10114126790	1037206552414	?
30	361340	86004800	13604287706	1519678218528	?
31	413540	105919940	18105920006	2195518394830	?
32	471200	129537600	23860611236	3130809484640	?
33	534688	157388960	31156143476	4410583469036	?
34	604384	190060544	40333505448	?	?
35	680680	228197664	51794268148	?	?
36	763980	272508504	66009149958	?	?
37	854700	323767788	83526964218	?	?
38	953268	382821120	104984952954	?	?
39	1060124	450588876	131119515534	?	?
40	1175720	528070800	162778537232	?	?

Zde je link na samotný "n-queens problem":
A000170 - NQ NxN - počty řešení na šachovnici NxN (Ways of placing n nonattacking queens on n x n board).

1.2) Queens on board k x n - Dámy na šachovnici k x n

2 Queens, board 2xn: (n-1)(n-2)

3 Queens, board 3xn: (n-3)(n²-6n+12), (E.Pauls, 1874)

4 Queens, board 4xn: n⁴-18n³+139n²-534n+840, n>=7, (M.Tarry, 1890)

5 Queens, board 5xn: n⁵-30n⁴+407n³-3098n²+13104n-24332, n>=11, (V.Kotesovec, 1992)

6 Queens, board 6xn: n⁶-45n⁵+943n⁴-11755n³+91480n²-418390n+870920, n>=17 (V.Kotesovec, 1992)

7 Queens, board 7xn: n⁷-63n⁶+1879n⁵-34411n⁴+417178n³-3336014n²+16209916n-36693996, n>=23 (V.Kotesovec, 1992)

8 Queens, board 8xn: n⁸-84n⁷+3378n⁶-85078n⁵+1467563n⁴-17723656n³+145910074n²-745654756n+1802501048, n>=31 (V.Kotesovec, 3.2.2010)

Obecně mají polynomy tvar: n^k - 3k(k-1)/2*n^k-1 + (9k⁴/8-29k³/12-k²/8+23k/12-1/4+(-1)^k/4)*n^k-2 - ...
(sekvence u třetího členu by tedy měla pokračovat takto: 0, 2, 30, 139, 407, 943, 1879, 3378, 5626, 8840, ...)
Koeficient u n^k-1 jsem odhadl již v roce 1992, koeficient u n^k-2 odvodil Ludovit Lačný v roce 2001, viz články "150 rokov problému osmich dám", L. Lacny, Pat a Mat 32/2001, str. 17-20 a Co nového v problému N - dam (What's new in N-queens problem), V. Kotesovec, Pat a Mat 32/2001, str.20-21. Nyní jsem tento vzorec potvrdil jinou metodou.

Tyto vzorce se dostaly i do OEIS
A061989 - 3Q 3xN
A061990 - 4Q 4xN
A061991 - 5Q 5xN
A061992 - 6Q 6xN
A061993 - 7Q 7xN
A172449 - 8Q 8xN

O autorech vzorců pro k=3 a k=4 se zmiňuje Wilhelm Ahrens ve své knize Mathematische Unterhaltungen und Spiele (vydání z roku 1921) na str.277.
Vzorec pro k=3 publikoval E.Pauls, "Das Maximalproblem der Damen auf dem Schachbrette", Deutsche Schachzeitung, 1874, str.261-263
Vzorec pro k=4 publikoval M. Harold Tarry na kongresu francouzských matematiků v roce 1890 v Limoges. Ve své přednášce uvedl i vzorce pro k=2 a k=3 a je proto v literatuře občas uváděn i jako autor těchto vzorců (vzorec pro k=3 však vymyslel již v roce 1874 E.Pauls). V Intermédiaire des Mathématiciens 1903, str.297-8 (str.682 v PDF) potom Tarry vyzval matematiky k nalezení obdobného vzorce pro šachovnici 5 x n, nikdo však takový vzorec nenalezl. Tento problém pak vyřešil až Václav Kotěšovec v roce 1992.

Poznámka: Ke stejným výsledkům (pro k=2,3,4,5,6) došli v článku Nonattacking queens in a rectangular strip (PDF) (na str.16) Thomas Zaslavsky, Seth Chaiken a Christopher R.H. Hanusa (2009). Bohužel jejich další výsledky (uvedené v tomto článku) pro střelce, jezdce a tátoše jsou chybné, protože uvažovali jen taková rozmístění, kde na každém sloupci stojí právě 1 kámen. To platí pro dámy a věže, ale v případě jiných kamenů může stát na jednom sloupci 2 i více neohrožujících se kamenů stejných hodnot. Formulas for queens and rooks in this article are same, but for bishops, knights and nightriders with additional condition "there is to be one piece in each row".

Jelikož vzorce pro rozmístění k dam na šachovnici kxn platí vždy až od jistého n, jsou v následující tabulce uvedeny počty i pro malá n, kde vzorce ještě neplatí (červená čísla). Sloupec vpravo představuje počty rozmístění vzájemně se neohrožujících n dam na šachovnici nxn (jehož speciálním případem je známý problém 8 dam, který vyřešil již v roce 1850 slavný matematik Gauss). Odvodit obecný vzorec se zatím nepodařilo a i jen tyto dílčí výsledky naznačují, o jak obtížný problém se jedná (porovnejte s diagonálou v tabulce).

n	k=2	k=3	k=4	k=5	k=6	k=7	k=8	n queens,nxn
2	0							0
3	2	0						0
4	6	4	2					2
5	12	14	12	10				10
6	20	36	46	40	4			4
7	30	76	140	164	94	40		40
8	42	140	344	568	550	312	92	92
9	56	234	732	1614	2292	2038	1066	352
10	72	364	1400	3916	7552	9632	7828	724
11	90	536	2468	8492	21362	37248	44148	2680
12	110	756	4080	16852	52856	120104	195270	14200
13	132	1030	6404	31100	117694	335010	707698	73712
14	156	1364	9632	54068	241484	835056	2211868	365596
15	182	1764	13980	89428	463038	1897702	6120136	2279184
16	210	2236	19688	141812	838816	3998456	15324708	14772512
17	240	2786	27020	216932	1448002	7907094	35312064	95815104
18	272	3420	36264	321700	2398292	14818300	75937606	666090624
19	306	4144	47732	464348	3832374	26512942	153942964	4968057848
20	342	4964	61760	654548	5935120	45562852	296590536	39029188884
21	380	5886	78708	903532	8941514	75580634	546621416	314666222712
22	420	6916	98960	1224212	13145292	121520020	968910732	2691008701644
23	462	8060	122924	1631300	18908302	190031678	1659114170	24233937684440
24	506	9324	151032	2141428	26670584	289879092	2754780934	227514171973736
25	552	10714	183740	2773268	36961170	432420154	4449361442	2207893435808352
26	600	12236	221528	3547652	50409604	632159540	7009572728	22317699616364044
27	650	13896	264900	4487692	67758182	907376502	10796663102	?
28	702	15700	314384	5618900	89874912	1280833348	16292133888	?
29	756	17654	370532	6969308	117767194	1780569602	24128511810	?
30	812	19764	433920	8569588	152596220	2440786884	35125842896	?
31	870	22036	505148	10453172	195692094	3302829550	50334575910	?
32	930	24476	584840	12656372	248569672	4416266132	71085565752	?
33	992	27090	673644	15218500	312945122	5840076618	99047961338	?
34	1056	29884	772232	18181988	390753204	7643950612	136295785608	?
35	1122	32864	881300	21592508	484165270	9909701414	185384054238	?
36	1190	36036	1001568	25499092	595607984	12732801060	249435319880	?
37	1260	39406	1133780	29954252	727782762	16224041362	332237569362	?
38	1332	42980	1278704	35014100	883685932	20511325988	438354441528	?
39	1406	46764	1437132	40738468	1066629614	25741598622	573248773718	?
40	1482	50764	1609880	47191028	1280263320	32082912244	743420525208	?

1.3) Conjectures - Hypotézy o funkci Q(n) pro n ® Ą

Jeden z nejzajímavějších článků o problému N-dam je Igor Rivin, Ilan Vardi and Paul Zimmermann: The n-Queens Problem, The American Mathematical Monthly, 101 (7/1994), str.629-639. Autoři zde analyzují "klasický" problém N-dam a počet různých pozic označují Q(n). Pro mnohé bude překvapující, že neohrožující se dámy je možné rozestavit též na prstencové šachovnici (toroidal board) pro některá lichá n. Tuto funkci označují T(n).
(poznámka: Bernd Eickenscheidt dokázal v článku Das n-Damen-Problem auf dem Zylinderbrett (feenschach 50/1980, str.382-5), že v případě válcové nebo prstencové šachovnice má problém n-dam řešení jen pro taková n, která nejsou dělitelná 2 ani 3). Jak jsem však zjistil v literatuře, důkaz tohoto tvrzení provedl mnohem dříve již Polya.

1) Rivin, Vardi a Zimmermann vyslovují hypotézu o průběhu těchto funkcí. Obě funkce jsou podle nich řádu n^an, kde konstanta a < 1. Jaká je přesně hodnota obou konstant pro tyto funkce však není známo. (hodnoty jsem doplnil o aktuální výsledky, tehdy jen do n=20)

2) Jak se zdá, byla tato hypotéza vyvrácena - Dronninger pa et skakbrat - článek v dánštině z 27.9.2000, jehož autorem je Birger Nielsen. Vyslovuje zde hypotézu, že funkce Q(n) je řádu Q(n) ~ n!*p^(n-1), kde p=0.3885... Dokládá to výpočty pro N až do 23 a hodnota p je mimořádně stabilní (na rozdíl od konstant ve výše citovaném článku), z čehož lze usuzovat, že řada je možná konvergentní. Naprosto unikátní objev! (viz hodnoty v tabulce dále)

3) 10.11.2002 vyslovil podobnou hypotézu Benoit Cloitre, podle něj funkce 1/n*log(n!/Q(n)) pro n®Ą konverguje ke konstantě C~0.90... (added 10.12.2004). Je zajímavé, že mezi touto konstantou C a konstantou P z hypotézy B.Nielsena platí (pro n®Ą) jednoduchý vztah c=-log(p). Takže pokud p=0.3885..., muselo by být c=0.9454...

4) Další pozoruhodný výsledek publikovali 28.8.2008 Cheng Zhang and Jianpeng Ma. V článku Counting Solutions for the N-queens and Latin Square Problems by Efficient Monte Carlo Simulations (PDF) došli pomocí simulací metodou Monte Carlo k (zatím asi nejpřesnějšímu) vztahu:
log (n!/Q(n)) ~ 0.944001*n - 0.937
s maximální chybou 0.02 (pro n > 100)
Zatímco předchozí hypotézy vznikaly na základě pokusů o extrapolaci ze známých (přesných) výsledků, tedy pouze z něco přes 20 čísel, tento výsledek má jiný charakter. Autoři simulovali problém až do šachovnic N x N, kde N=10000. Takové výsledky, podložené teorií pravděpodobnosti, mají proto větší váhu. Jejich metoda nám sice nepřinese přesné hodnoty Q(n) pro jednotlivá N, ale u odhadů lze stanovit rozsah pravděpodobné chyby. Je to proto první rovnice, která není jen hypotézou, ale opravdovým výsledkem řešení tohoto problému. (viz hodnoty v tabulce dále)
Tento výsledek je téměř shodný s hypotézou Birger Nielsena, neboť přepočtem vychází Q(n) ~ e^0.937*n!*e^-0.944*n
po úpravách z toho dostaneme Q(n) ~ 2.552*n!*0.389ⁿ
což se dá napsat také jako Q(n) ~ 0.993*n!*0.389^(n-1)
a nyní už je na místě otázka, zda konstanta 0.993 nemá být spíš 1 ?
Pokud bychom obráceně vyšli z (elegantnější) hypotézy Birger Nielsena, lze ji převést do tvaru
log (n!/Q(n)) ~ 0.9454*n - 0.9454
Rozdíl je tedy pouze v tom, že zde jsou obě konstanty shodné.
A pro "c" ze vztahu Benoit Cloitrea dostáváme limitně přímo hodnotu 0.944001..., resp. 0.9454...

n	T(n)	log T(n)/(n log n)	Q(n)	log Q(n)/(n log n)	(Q(n)/n!)^(1/(n-1))	1/n*log(n!/Q(n))	(0.937+log(n!/Q(n)))/n
1	1	-	1	-	-	-	-
2	0	-	0	-	-	-	-
3	0	-	0	-	-	-	-
4	0	-	2	0.12500	0.436790	0.6212266624	0.855476662
5	10	0.28613	10	0.28613	0.537285	0.4969813299	0.684381330
6	0	-	4	0.12895	0.353953	0.8654928084	1.021659475
7	28	0.24463	40	0.27081	0.446620	0.6908974152	0.824754558
8	0	-	92	0.27181	0.419382	0.7603517907	0.877476791
9	0	-	352	0.29651	0.420095	0.7709107004	0.875021812
10	0	-	724	0.28597	0.388049	0.8519621180	0.945662118
11	88	0.16974	2680	0.29926	0.382559	0.8735214338	0.958703252
12	0	-	14200	0.32063	0.387578	0.8688514376	0.946934771
13	4524	0.25243	73712	0.33612	0.388542	0.8726340743	0.944710997
14	0	-	365596	0.34669	0.385792	0.8844240718	0.951352643
15	0	-	2279184	0.36039	0.387849	0.8839962227	0.946462889
16	0	-	14772512	0.37213	0.388976	0.8852238369	0.943786337
17	140692	0.24612	95815104	0.38156	0.388506	0.8898319151	0.944949562
18	0	-	666090624	0.39050	0.388371	0.8932504953	0.945306051
19	820496	0.24341	4968057848	0.39908	0.388602	0.8954520716	0.944767861
20	0	-	39029188884	0.40703	0.388822	0.8974020412	0.944252041
21	0	-	314666222712	0.41408	0.388575	0.9002552664	0.944874314
22	0	-	2691008701644	0.42087	0.388583	0.9022838241	0.944874733
23	128850048	0.25894	24233937684440	0.42734	0.388717	0.9038217572	0.944560888
24	0	-	227514171973736	0.43341	0.388823	0.9052706563	0.944312323
25	1957725000	0.26586	2207893435808352	0.43904	0.388796	0.9069115985	0.944391599
26	0	-	22317699616364044	0.44438	0.388795	0.9083671268	0.944405588
27	0	-	?	?	?	?	?
28	0	-	?	?	?	?	?
29	605917055356	0.27782	?	?	?	?	?
30	0	-	?	?	?	?	?
31	13404947681712	0.28394	?	?	?	?	?
32	0	-	?	?	?	?	?
33	0	-	?	?	?	?	?
34	0	-	?	?	?	?	?
35	?	?	?	?	?	?	?
.
Ą		®1 ?		®1 ?	®0.3885... ?	®0.9454... ?	®0.9440... ?

Updated for n=24 (4.12.2004), for n=25 (25.6.2005) and for n=26 (21.1.2010)

Pokud přijmeme hypotézu B.Nielsena, pak s použitím Stirlingova vzorce n! ~ nⁿ e^-n Ö(2 p n) dostaneme

lim
n® Ą

ć
ç
č

log Q(n)

n log(n)

ö
÷
ř

a tím pádem obě konstanty z hypotézy Rivin+Vardi+Zimmermann ®1, což tuto hypotézu znehodnocuje.

Odkazy na jiné stránky s podobnou problematikou links

1.4) Queens on toroidal board n x n - Dámy na prstencové šachovnici n x n

2 Queens, toroidal board nxn:
n²(n-2)²/2, pro n sudé (even),
n²(n-1)(n-3)/2, pro n liché (odd)

3 Queens, toroidal board nxn:
n²(n-2)(n-4)(n²-6n+12)/6, pro n sudé (even), (V. Kotesovec, 31.1.2010)
n²(n-1)(n-3)(n²-8n+18)/6, pro n liché (odd), (V. Kotesovec, 31.1.2010)

4 Queens, toroidal board nxn:
Počet rozmístění 4 neohrožujících se dam na prstencové šachovnici se dá vyjádřit buď tímto jedním vzorcem nebo 12 vzorci odpovídajícími velikosti šachovnice (podle zbytku po dělení 12). Někoho možná překvapí funkce cosinus ve vzorci, taková řešení však jsou obvyklá, pokud charakteristická rovnice pro příslušnou diferenční rovnici má imaginární kořeny. Výsledné hodnoty jsou vždy celočíselné a nejmenší perioda je 12.
(n⁸/24 - n⁷ + 245n⁶/24 - 113n⁵/2 + 2843n⁴/16 - 593n³/2 + 4757n²/24) + (n⁶/8 - 5n⁵/2 + 305n⁴/16 - 129n³/2 + 629n²/8)*(-1)ⁿ + 8n²*COS(2*pi*n/3)/3 + 9n²*COS(pi*n/2)/2, (V. Kotesovec, 5.2.2010)

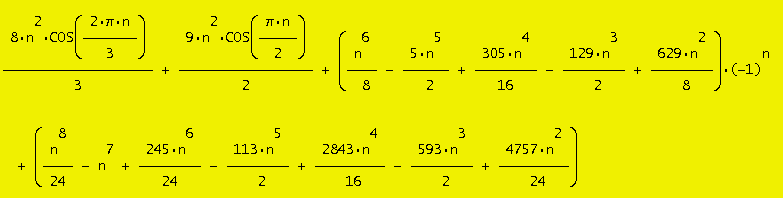
explicit formula by Vaclav Kotesovec

4 Queens toroidal nxn n=	n⁸	n⁷	n⁶	n⁵	n⁴	n³	n²	n¹	n⁰
12a	1/24	-1	31/3	-59	787/4	-361	284	0	0
12a+1	1/24	-1	121/12	-54	1269/8	-232	473/4	0	0
12a+2	1/24	-1	31/3	-59	787/4	-361	271	0	0
12a+3	1/24	-1	121/12	-54	1269/8	-232	489/4	0	0
12a+4	1/24	-1	31/3	-59	787/4	-361	280	0	0
12a+5	1/24	-1	121/12	-54	1269/8	-232	473/4	0	0
12a+6	1/24	-1	31/3	-59	787/4	-361	275	0	0
12a+7	1/24	-1	121/12	-54	1269/8	-232	473/4	0	0
12a+8	1/24	-1	31/3	-59	787/4	-361	280	0	0
12a+9	1/24	-1	121/12	-54	1269/8	-232	489/4	0	0
12a+10	1/24	-1	31/3	-59	787/4	-361	271	0	0
12a+11	1/24	-1	121/12	-54	1269/8	-232	473/4	0	0

Rekurentní vztah:
a_n = -a_n-1+3a_n-2+6a_n-3+3a_n-4-9a_n-5-20a_n-6-11a_n-7+15a_n-8+40a_n-9+31a_n-10-15a_n-11-53a_n-12-50a_n-13+50a_n-15+53a_n-16+15a_n-17-31a_n-18-40a_n-19-15a_n-20+11a_n-21+20a_n-22+9a_n-23-3a_n-24-6a_n-25-3a_n-26+a_n-27+a_n-28
(pro n>=29, člen n-14 má koeficient 0)

5 Queens, toroidal board nxn:
1/120*n¹⁰-1/3*n⁹+143/24*n⁸-373/6*n⁷+99377/240*n⁶-3603/2*n⁵+119627/24*n⁴-23833/3*n³+16342/3*n²
+ (1/24*n⁸-3/2*n⁷+1111/48*n⁶-391/2*n⁵+7595/8*n⁴-2487*n³+8032/3*n²)*(-1)ⁿ
+ (9/2*n⁴-78*n³+374*n²)*COS(pi*n/2)
+ (8/3*n⁴-128/3*n³+656/3*n²)*COS(2*pi*n/3)
+ 80/3*n²*COS(pi*n/3)
+ 16/5*n²*COS(2*pi*n/5)
+ 16/5*n²*COS(pi*n/5)*(-1)ⁿ, (V. Kotesovec, 24.2.2010)

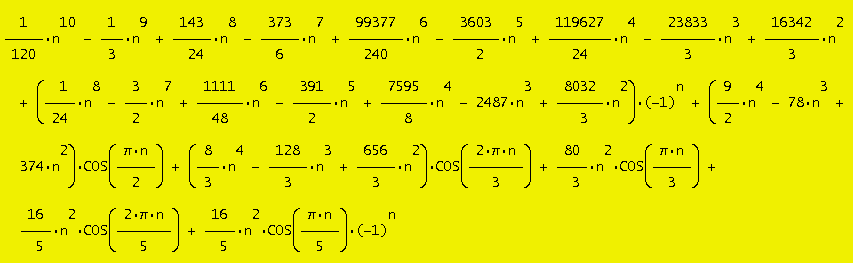
explicit formula by Vaclav Kotesovec

Rekurentní vztah:
a_n = -3a_n-1-5a_n-2-5a_n-3+2a_n-4+17a_n-5+37a_n-6+49a_n-7+35a_n-8-16a_n-9-101a_n-10-185a_n-11-215a_n-12-139a_n-13+56a_n-14+321a_n-15+544a_n-16+588a_n-17+368a_n-18-99a_n-19-656a_n-20-1069a_n-21-1111a_n-22-689a_n-23+84a_n-24+929a_n-25+1488a_n-26+1506a_n-27+939a_n-28-939a_n-30-1506a_n-31-1488a_n-32-929a_n-33-84a_n-34+689a_n-35+1111a_n-36+1069a_n-37+656a_n-38+99a_n-39-368a_n-40-588a_n-41-544a_n-42-321a_n-43-56a_n-44+139a_n-45+215a_n-46+185a_n-47+101a_n-48+16a_n-49-35a_n-50-49a_n-51-37a_n-52-17a_n-53-2a_n-54+5a_n-55+5a_n-56+3a_n-57+a_n-58, n>58

OEIS linky:
A172517 - 2Q toroidal NxN
A172518 - 3Q toroidal NxN
A172519 - 4Q toroidal NxN
A173775 - 5Q toroidal NxN

n	2 queens	3 queens	4 queens	5 queens
2	0	0	0
3	0	0	0	0
4	32	0	0	0
5	100	100	50	10
6	288	576	288	0
7	588	2156	2450	882
8	1152	7168	16384	13312
9	1944	17496	62208	85536
10	3200	41600	233600	561440
11	4840	82280	638880	2276736
12	7200	161280	1755072	9471744
13	10140	280540	3901534	27991470
14	14112	486080	8772176	85725696
15	18900	774900	17051850	209107890
16	25088	1232896	33507328	525062144
17	32368	1844976	59175640	1116665944
18	41472	2757888	105557904	2437807104
19	51984	3933456	173570244	4691672964
20	64800	5606400	287904000	9234168960
21	79380	7699860	447885774	16462896030
22	96800	10570560	702042000	29919532544
23	116380	14081980	1044894554	50215537658
24	139392	18754560	1565385984	85687824384
25	165000	24365000	2247132500	136944081500
26	194688	31647616	3244194304	222030242304
27	227448	40258296	4519015596	340788006540
28	264992	51204608	6326171264	529663525888
29	306124	63979916	8590557654	785790131238
30	352800	79934400	11716668000	1178695280160
31	403620	98348740	15567229390	1698736557198
32	460800	120995840	20763631616	2472214872064
33	522720	146884320	27070819380	3475005224724
34	591872	178301440	35416066816	4927131387904
35	666400	213914400	45416742700	6776457658740
36	749088	256628736	58421984832	9392614619904
37	837828	304690116	73833633570	12672854468658
38	935712	361739328	93571390608	17218696084992
39	1040364	425508876	116731332198	22840988228838
40	1155200	500505600	145991424000	30491340899840
41	1277560	583844920	180024039020	39839128802924
42	1411200	681045120	222499677456	52352705728512
43	1553160	788487560	271515768944	67478117820624
44	1707552	912862720	332023922560	87430668092416
45	1871100	1049687100	401355457650	111314431376010
46	2048288	1207000256	486095146064	142404689281536
47	2235508	1379308436	582569828310	179295582644310
48	2437632	1576194048	699422837760	226741660434432

(Hodnoty pro k=4 byly ověřeny výpočtem až do n=120)

Poznámka: Z matematického pohledu je zajímavější prstencová šachovnice než válcová (z šachového pohledu je to asi obráceně). V případě dam, věží nebo střelců jsou výsledky pro prstencovou šachovnici shodné jako pro válcovou šachovnici. V případě bodových kamenů (např. jezdců) to ale neplatí.
For queens, rooks and bishops are results for toroidal and cylindrical chessboard same, but for leapers (for example knights) are results different.

Zde je link na samotný "n-queens problem" na prstencové šachovnici:
A007705 - NQ NxN - počty řešení na prstencové šachovnici (Nonattacking queens on a 2n+1 x 2n+1 toroidal board).

2.1) Kings on board n x n - Králové na šachovnici n x n

Velmi zajímavý (i když poněkud jiný) je problém rozmístění neohrožujících se králů.

2 Kings, board nxn: (n-1)(n-2)(n²+3n-2)/2, (E. Lucas, 1891)

3 Kings, board nxn: (n-1)(n-2)(n⁴+3n³-20n²-30n+132)/6, (E. Landau, before 1901)

4 Kings, board nxn: (n⁸-54n⁶+72n⁵+995n⁴-2472n³-5094n²+21480n-17112)/24, n>=3, (K.Fabel + K.Soltsien, 1966)

5 Kings, board nxn: (n-4)(n⁹+4n⁸-74n⁷-176n⁶+2411n⁵+1844n⁴-38194n³+18944n²+236520n-316320)/120, n>=4, (V.Kotesovec, 1992)

6 Kings, board nxn: (n¹²-135n¹⁰+180n⁹+7465n⁸-18840n⁷-202665n⁶+751860n⁵+2442334n⁴-13441200n³-3643800n²+89860320n-108217440)/720, n>=5, (V. Kotesovec, 27.1.2010)

Obecný vzorec není znám, ale první členy polynomu mají vždy tvar n^2k/k! - 9n^2k-2/2/(k-2)! + 6n^2k-3/(k-2)! ...

Tyto vzorce jsou i v OEIS
A061995 - 2K NxN
A061996 - 3K NxN
A061997 - 4K NxN
A061998 - 5K NxN
A172158 - 6K NxN

Viz Edouard Lucas: Théorie des nombres (1891), vzorec pro počet rozmístění 2 neohrožujících se králů najdeme na str.98 (ve vzorci vypadlo "/2"), viz též Edouard Lucas: Récréations mathématiques (1894) str.132 (i zde vypadlo "/2", v následujících dvou knihách Ahrense a Fabela je tento vzorec uveden správně).
Vzorec pro k=3 uvádí v knize Mathematische unterhaltungen und spiele (1901) Wilhelm Ahrens na str.155 s tím, že mu jej v dopise zaslal Edmund Landau.
Vzorec pro k=4 uvádí v knize Schach und Zahl (1966) na str.54 Karl Fabel.

n	2 kings	3 kings	4 kings	5 kings	6 kings
2	0	0	0
3	16	8	1	0	0
4	78	140	79	0	0
5	228	964	1987	1974	978
6	520	3920	16834	42368	62266
7	1020	11860	85275	397014	1220298
8	1806	29708	317471	2326320	12033330
9	2968	65240	962089	10087628	77784658
10	4608	129984	2515262	35464464	377818258
11	6840	240240	5882109	106783320	1492665418
12	9790	418220	12605095	285336128	5042436754
13	13596	693308	25175191	693331146	15062292834
14	18408	1103440	47443474	1558986816	40736208186
15	24388	1696604	85152487	3286192514	101489568538

2.2) Kings on board k x n - Králové na šachovnici k x n

2 kings, board 2xn: 2(n-1)(n-2)
3 kings, board 3xn: (n-2)(9n²-45n+70)/2, n>=2, (V. Kotesovec, 27.1.2010)
4 kings, board 4xn: (64n⁴-720n³+3347n²-7569n+6894)/6, n>=3, (V. Kotesovec, 27.1.2010)
5 kings, board 5xn: (625n⁵-9750n⁴+66415n³-247626n²+504664n-446544)/24, n>=4, (V. Kotesovec, 27.1.2010)
6 kings, board 6xn: 2(162n⁶-3240n⁵+29160n⁴-151830n³+483798n²-895085n+749335)/5, n>=5, (V. Kotesovec, 27.1.2010)
7 kings, board 7xn: (117649n⁷-2873997n⁶+32197753n⁵-215350695n⁴+932130286n³-2618213868n²+4424623272n-3468569760)/720, n>=6, (V. Kotesovec, 28.1.2010)
8 kings, board 8xn: (1048576n⁸-30277632n⁷+406210560n⁶-3319585920n⁵+18136811049n⁴-68048382318n³+171628664735n²-266425935930n+194935658400)/2520, n>=7, (V. Kotesovec, 30.1.2010)

První členy těchto vzorců mají obecně tvar (kn)^k/k! - 3(k-1)(3k-2)(kn)^k-1/2/k! + ...

OEIS linky:
A172202 - 3 kings 3 X n
A172203 - 4 kings 4 X n
A172204 - 5 kings 5 X n
A172205 - 6 kings 6 X n
A172206 - 7 kings 7 X n
A172261 - 8 kings 8 X n

n	2 kings	3 kings	4 kings	5 kings	6 kings	7 kings	8 kings
2	0	0	0	0	0	0	0
3	4	8	9	15	16	24	25
4	12	34	79	194	408	926	1847
5	24	105	454	1974	8544	37282	162531
6	40	248	1566	9856	62266	394202	2501726
7	60	490	4103	34475	291908	2484382	21243084
8	84	858	9009	95466	1021254	10999618	119138166
9	112	1379	17484	224589	2916232	38168864	502726650
10	144	2080	30984	468854	7179314	110899878	1724809105
11	180	2988	51221	893646	15790572	281638602	5059647669
12	220	4130	80163	1585850	31795390	643766432	13132889249
13	264	5533	120034	2656976	59638832	1352358921	30905051345
14	312	7224	173314	4246284	105546666	2651129458	67124176002
15	364	9230	242739	6523909	177953044	4906381466	136380034610
16	420	11578	331301	9693986	287974838	8648792662	261909043488
17	480	14295	442248	13997775	449932632	14623854922	479315827404
18	544	17408	579084	19716786	681918370	23851793294	841394145399
19	612	20944	745569	27175904	1006409660	37697787702	1424246670499
20	684	24930	945719	36746514	1450930734	57953320884	2334919892115
21	760	29393	1183806	48849626	2048760064	86929476107	3720787187147
22	840	34360	1464358	63959000	2839684634	127563008202	5780929883024
23	924	39858	1792159	82604271	3870800868	183536011462	8779782913128
24	1012	45914	2172249	105374074	5197362214	259410007946	13063328442266
25	1104	52555	2609924	132919169	6883673384	360775279732	19078137617070

2.3) Kings on boards of various size - Králové na šachovnicích jiných rozměrů

Maximální možný počet neohrožujících se králů na šachovnici n x n je n²/4 (pro n sudé) a (n²+1)/4 (pro n liché), více viz Kings Problem

Řadu výsledků najdeme v knize Schach und Zahl, 1966, jejíž autoři jsou E.Bonsdorff, K.Fabel, O.Riihimaa. Speciální je případ, kdy králů je na šachovnici právě tolik, že každý musí být ve svém pevném čtverci velikosti 2x2. Celkový počet králů je v těchto případech roven vždy čtvrtině počtu polí příslušné šachovnice.

Number of ways to place n nonattacking kings on a 2 x 2n chessboard.
V citované knize na str.53 najdeme (pro tento jednoduchý případ) vzorec:
f₁(n) = (n+1)*2ⁿ

A061593 - Number of ways to place 2n nonattacking kings on a 4 x 2n chessboard.
Na str.53 knihy Schach und Zahl (1966) nalezneme i excelentní vzorec pro rozmístění 2m neohrožujících se králů na šachovnici 2m x 4, jehož autorem je C.Bandelow. Stejný vzorec najdeme v článku Nonattacking kings on a chessboard, D. E. Knuth, 1994.
f₂(n) = (17n-109)*3ⁿ+2*Fibonacci(2n+10)
Kdo by čekal v obecném vzorci Fibonacciho čísla? Explicitní tvar tohoto vzorce je
f₂(n) = (17n-109)*3ⁿ + 2/sqrt(5)*(((3+sqrt(5))/2)ⁿ⁺⁵ - ((3-sqrt(5))/2)ⁿ⁺⁵)
Ještě je možno poznamenat, že tato (poněkud divoká) funkce je řešením diferenční rovnice
a_n = 9a_n-1-28a_n-2+33a_n-3-9a_n-4

A061594 - Number of ways to place 3n nonattacking kings on a 6 x 2n chessboard
Herbert S. Wilf se dostal ještě trochu dál, když v článku The Problem of the Kings, Electronic Journal of Combinatorics (1995), uvedl pro šachovnici 6x2n a 3n neohrožujících se králů odhad:
f₃(n) = 231*n*4ⁿ - 2377*4ⁿ - 384*3ⁿ + O(1.707ⁿ)
Článek Non-attacking placements on chessboards (.ps), jehož autorem je Sergey Kitaev, má shodné výsledky a kromě králů řeší i rozmístění neohrožujících se pěšců na polích stejné barvy (number of nonattacking pawns, all of the same colour). V případě pěšců Sergey Kitaev a Toufik Mansour ještě došli k dalším výsledkům, které popisují v článku The Problem of the Pawns, Annals of Combinatorics (2004) (z článku je bohužel volně dostupný jen abstract). Jakási verze je k dispozici zde The problem of the pawns (2003)

Podařilo se mi najít přesný vzorec (exact formula by Vaclav Kotesovec, 5.2.2010):
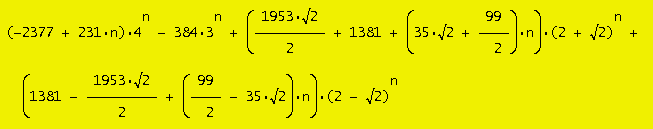
exact formula by Vaclav Kotesovec

f₃(n) = (231n-2377)*4ⁿ - 384*3ⁿ + (1953*sqrt(2)/2+1381+(35*sqrt(2)+99/2)*n)*(2+sqrt(2))ⁿ + (1381-1953*sqrt(2)/2+(99/2-35*sqrt(2))*n)*(2-sqrt(2))ⁿ
kde sqrt(2) = odmocnina ze 2. Je tedy vidět, že Wilfův odhad zbytku byl poněkud nepřesný, správně mělo být + O(n*3.4142ⁿ)

Příslušná diferenční rovnice je
a_n=19a_n-1 - 148a_n-2 + 604a_n-3 - 1364a_n-4 + 1644a_n-5 - 928a_n-6 + 192a_n-7

A173782 - Number of ways to place 4n nonattacking kings on a 8 x 2n chessboard
Herbert S. Wilf ve svém článku z roku 1995 dále uvádí, že pro 4n králů na šachovnici 8 x 2n má první člen podobné rovnice tvar
f₄(n) ~ (7963567/2610)*n*5ⁿ + ...

Pro případ 4n králů na šachovnici 8 x 2n jsem odvodil vytvořující funkci (Generating function) (V. Kotesovec, 24.2.2010):
x*(22500x¹⁶-382125x¹⁵+2723005x¹⁴-10917322x¹³+27938661x¹²-48873227x¹¹+60780149x¹⁰-54895129x⁹+36368733x⁸-17776175x⁷+6499001x⁶-1854479x⁵+446565x⁴-94300x³+15732x²-1673x+80) / ((1-x)(x²-4x+1)(x³-6x²+5x-1)(4x-1)(5x-1)²(3x²-5x+1)²(5x²-5x+1)²)

a rekurentní vzorec (Recurrence:)
a_n = 44a_n-1-887a_n-2+10855a_n-3-90083a_n-4+536398a_n-5-2365292a_n-6+7860674a_n-7-19852652a_n-8+38152568a_n-9-55523880a_n-10+60518766a_n-11-48502595a_n-12+27783210a_n-13-10888525a_n-14+2721025a_n-15-382125a_n-16+22500a_n-17, n>17

Vytvořující funkce není přímo explicitním vzorcem pro danou posloupnost, ale příslušná posloupnost z ní jde vytvořit tak, že vygenerujeme Taylorův rozvoj pro danou vytvořující funkci a jednotlivé členy této posloupnosti jsou koeficienty tohoto rozvoje. Přesněji: člen a_n posloupnosti je n-tá derivace vytvořující funkce v nule dělena n faktoriál. Obvykle není tento postup pro výpočet členů posloupnosti ten nejefektivnější, ale v případech, kdy je obtížné určit explicitní vzorec, je vyjímečně takový postup rychlejší. Ohledně vytvořujících funkcí je třeba ještě poznamenat, že z jejího jmenovatele lze snadno odvodit rekurentní vzorec, který vznikne roznásobením všech členů jmenovatele a nahrazením všech členů x^k výrazy a_n-k.
Jmenovatel (denominator) pak dále určuje tvar parciálních členů řešení příslušné diferenční rovnice. Zde ho naopak potřebujeme ve faktorizovaném tvaru a pokud je kořen takto vzniklé rovnice t, je jedním z parciálních řešení funkce 1/tⁿ. Pokud tedy např. v případě této posloupnosti obsahuje jmenovatel vytvořující funkce člen (5x-1), odpovídá tomu kořen 1/5 a parciální člen řešení diferenční rovnice 5ⁿ.
Každé takovéto parciální řešení je třeba násobit polynomem (s neznámými koeficienty) jehož stupeň je roven násobnosti příslušného kořene - 1. V našem případě měl člen (5x-1)² stupeň 2, tvar příslušného parciálního řešení proto bude (f₀+f₁*n)* 5ⁿ, kde konstanty f₀ a f₁ budou určeny podle počátečních hodnot posloupnosti.
V případě, že má denominator (tzv. charakteristická rovnice) komplexní kořeny, je situace složitější. Pokud má rovnice kořen a+b*i (jak je známo, musí mít současně i komplexně sdružený a-bi), pak mají parciální řešení diferenční rovnice tvar
(a²+b²)^n/2 *COS(n*ATAN(b/a))
a
(a²+b²)^n/2 *SIN(n*ATAN(b/a))
Častým výrazem ve jmenovateli bývá např. člen x²+1, ze kterého dostáváme kořeny +i a -i, kterým odpovídají parciální řešení COS(pi*n) a SIN(pi*n). Tento případ je typický, pokud se odlišují vzorce na šachovnicích sudých a lichých rozměrů. Pro celá čísla je však člen SIN(pi*n) vždy roven 0 a člen COS(pi*n) lze nahradit příjemnějším výrazem (-1)ⁿ. O násobnostech kořenů platí totéž jako v případě kořenů reálných.

Tvar explicitního vzorce vyplývá ze jmenovatele vytvořující funkce, koeficienty jsem určil nejprve numericky:
f₄(n) = ("f0"+"f1"*n)*5ⁿ + "p3"*4ⁿ + "p4"
+ "p1"*(2-SQRT(3))ⁿ+"p2"*(2+SQRT(3))ⁿ
+ ("c0"+"c1"*n)*((5-SQRT(5))/2)ⁿ+("d0"+"d1"*n)*((5+SQRT(5))/2)ⁿ
+ ("a0"+"a1"*n)*((5-SQRT(13))/2)ⁿ+("b0"+"b1"*n)*((5+SQRT(13))/2)ⁿ
+ "x1"*(SQRT(3)/(2*(SQRT(3)-SQRT(7)*COS(ATAN(SQRT(3)/9)/3+pi/3))))ⁿ
+ "x2"*(SQRT(3)/(2*(SQRT(3)-SQRT(7)*SIN(ACOT(-SQRT(3)/9)/3))))ⁿ
+ "x3"*(SQRT(3)/(2*(SQRT(7)*COS(ATAN(SQRT(3)/9)/3)+SQRT(3))))ⁿ

x1=-0.26377035674015103140762...
x2=1775.680242270463563416958...
x3=0.000114426854513301676567...
a0=0.016247286549426572256187...
a1=0.004738824796414161533626...
b0=50967.32103081995944916738...
b1=2377.824321004263414898295...
c0=0.205693095526376627060778...
c1=0.011423393098813887747739...
d0=13320.19430690447362337293...
d1=-25.2114233930988138877477...
p1=-0.00264173363558122860165...
p2=-26046.7751360441421965491...
f0=-41306.0010866693090236490...
f1=3051.175095785440613026819...
p3=1290.666666666666666666666...
p4=-0.04166666666666666666666...

Pro konstanty x1,x2,x3 platí x1+x2+x3 = 252338184/142129
Některé z těchto koeficientů lze snadno vyjádřit i algebraicky, problémy však dělají 3 reálné kořeny kubické rovnice, které jde vyjádřit jen pomocí trigonometrických funkcí a takové výrazy se pak obtížně upravují a zjednodušují.

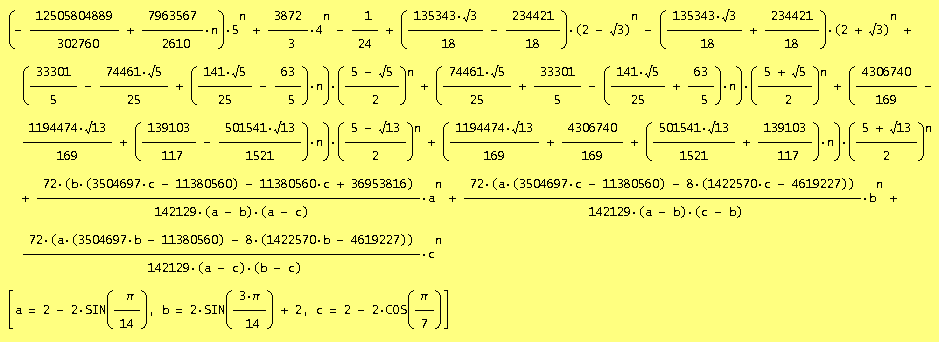
Tady je explicitní vzorec v algebraickém tvaru (V. Kotesovec, 25.2.2010): explicit formula by Vaclav Kotesovec

Konstanty a, b, c (převrácené hodnoty kořenů kubické rovnice x³-6x²+5x-1) mají tyto numerické hodnoty:
[a = 1.554958132087371191419255..., b = 3.246979603717467061021860..., c = 0.198062264195161747527865...]

Zde musím upozornit na různou implementaci funkce ArcCot v programu Mathematica7 pro záporné argumenty. Podle tohoto programu vyjde např. ArcCot(-1)=-pi/4, zatímco Derive6 dává svou funkcí ACOT(-1)=3*pi/4, což je správná hodnota (=right value), viz např. "Schaum's outlines - Trigonometry", str.139, Chapter 13 "Inverses of Trigonometric Functions". Pro kladné argumenty jsou výsledky totožné. Výše uvedený vzorec pracuje s interpretací ACOT.

A173783 - Number of ways to place 5n nonattacking kings on a 10 x 2n chessboard

Pro získání této funkce jsem
1) napsal poměrně jednoduchý program, který vygeneroval transformační matici (program je obecný pro libovolné m a vygenerování trvá jen pár vteřin)
2) bylo nutno provést inverzi této matice (pro m=5 velikosti 192 x 192).

Zajímavé je zde srovnání současných matematických programů, které zvládají výpočty na úrovni symbolických výrazů. Inverzi matice 192x192 zvládne "Derive 6" za 69 minut, "Matlab 7" za 7 minut a "Mathematica 7" za 10 minut, musí se ale nastavit Method -> "OneStepRowReduction" (což není předdefinovaná hodnota). Při použití stejné metody a funkce "LinearSolve" (místo inverze matice) se dostane "Mathematica 7" dokonce těsně pod 1 minutu, tato metoda však selhává pro větší matice (např. 448x448), protože je nesmírně paměťově náročná, nestačí ani 4 GB RAM. Proto se jako nejvhodnější pro symbolické výpočty s velkými poli zdá program "Matlab 7" (inverze matice je v jeho případě nezbytná, protože analogická funkce "linsolve" lze použít jen pro numerické výpočty). Pro výpočet determinantu matice na symbolické úrovni je naopak nejrychlejší "Mathematica 7" (např. determinant 448x448 zvládne za pouhých 12 vteřin).

Vytvořující funkce (Generating function) (V. Kotesovec, 24.2.2010):

2x*(292626432x³⁰-7695378432x²⁹+94084706304x²⁸-712519981056x²⁷+3757888797696x²⁶-14715718076160x²⁵+44556058968960x²⁴-107273952716256x²³+209645023363168x²²-337824014576768x²¹+454329405135504x²⁰-514643686425920x¹⁹+494203416082160x¹⁸-403847150294172x¹⁷+281135354205764x¹⁶-166453721883480x¹⁵+83456844800670x¹⁴-35182845104124x¹³+12345883162136x¹²-3557728594620x¹¹+827346101101x¹⁰-152042822189x⁹+21726065190x⁸-2499103126x⁷+289877178x⁶-45817212x⁵+7810422x⁴-1012942x³+86355x²-4311x+96) / ((1-2x)(x²-4x+1)(4x-1)(6x-1)²(2x²-4x+1)(2x²-5x+1)(4x²-6x+1)²(6x²-6x+1)²(7x²-6x+1)²(2x³-8x²+6x-1)(3x³-9x²+6x-1)²)

Rekurentní vzorec:
a_n = 85a_n-1-3441a_n-2+88303a_n-3-1613002a_n-4+22327010a_n-5-243429637a_n-6+2145452227a_n-7-15565947848a_n-8+94202823084a_n-9-480152808502a_n-10+2075863416838a_n-11-7651361422835a_n-12+24128330540449a_n-13-65240466585284a_n-14+151411770874148a_n-15-301613628545814a_n-16+515173613407544a_n-17-753006145475828a_n-18+939001403456656a_n-19-994821988961592a_n-20+890558910282768a_n-21-668920434927504a_n-22+417832289937792a_n-23-214574645977920a_n-24+89258591798784a_n-25-29486236792320a_n-26+7526493775872a_n-27-1426182018048a_n-28+188221833216a_n-29-15390756864a_n-30+585252864a_n-31, n>31

Tvar explicitního vzorce vyplývá ze jmenovatele vytvořující funkce, koeficienty jsem vypočítal nejprve numericky. Nejzajímavější je koeficient "a1" u členu s nejvyšší váhou, který určuje chování funkce pro n jdoucí do nekonečna.
f₅(n) = ("a0"+"a1"*n)*6ⁿ + "b0"*4ⁿ
+"c0"*2ⁿ+"d0"*(2+SQRT(3))ⁿ+"d1"*(2-SQRT(3))ⁿ
+"e0"*(2+SQRT(2))ⁿ+"e1"*(2-SQRT(2))ⁿ
+"f0"*((5+SQRT(17))/2)ⁿ+"f1"*((5-SQRT(17))/2)ⁿ
+("g0"+"g1"*n)*(3+SQRT(5))ⁿ+("g2"+"g3"*n)*(3-SQRT(5))ⁿ
+("h0"+"h1"*n)*(3+SQRT(3))ⁿ+("h2"+"h3"*n)*(3-SQRT(3))ⁿ
+("i0"+"i1"*n)*(3+SQRT(2))ⁿ+("i2"+"i3"*n)*(3-SQRT(2))ⁿ
+"j1"*(1/(4/3-2*SQRT(7)*COS(ATAN(3*SQRT(111)/67)/3+pi/3)/3))ⁿ
+"j2"*(1/(4/3-2*SQRT(7)*SIN(ACOT(-3*SQRT(111)/67)/3)/3))ⁿ
+"j3"*(1/(2*SQRT(7)*COS(ATAN(3*SQRT(111)/67)/3)/3+4/3))ⁿ
+("k1"+"k2"*n)*(SQRT(3)/(2*COS(pi/18)+SQRT(3)))ⁿ
+("k3"+"k4"*n)*(SQRT(3)/(SQRT(3)-2*SIN(2*pi/9)))ⁿ
+("k5"+"k6"*n)*(SQRT(3)/(SQRT(3)-2*SIN(pi/9)))ⁿ

"a0"=-678713.914029838744250543...
"a1"=40881.99638391654123778175...
"b0"=-34068
"c0"=-1.16666666666666666666666...
"d0"=-51446.4849177672922717349...
"d1"=-0.00015892757463292217669...
"e0"=-10107.4970977440220279807...
"e1"=-0.00144453003045015334953...
"f0"=-684492.238277441947051457...
"f1"=-0.01172255805294854295976...
"g0"=926641.4858544337556115334...
"g1"=38562.08938946586577992332...
"g2"=0.050993455065133123680865...
"g3"=0.004591899029712395988044...
"h0"=-62326.0581297792402651458...
"h1"=723.9986187818953543472362...
"h2"=0.058129779240265145814576...
"h3"=0.001381218104645652763714...
"i0"=451705.3288256058621516918...
"i1"=-464.669820354223846560962...
"i2"=-105.212207530060402420677...
"i3"=-1.61589393149043915332353...
"j1"=0.681071493211076255730644...
"j2"=-5142.77599692595609626251...
"j3"=0.015530347678857435892035...
"k1"=-0.01214865752499437628069...
"k2"=0.001607392808026484702220...
"k3"=147951.3666730136147131534...
"k4"=1491.573767571326753514216...
"k5"=105.3857202386842498663759...
"k6"=-2.43062880321861841180229...

Pro konstanty platí j1+j2+j3 = -2720160/529, k1+k3+k5 = 4989255563912/33698267, k2+k4+k6 = 1398248840/938961

První část vzorce jde vyjádřit i v algebraickém tvaru (V. Kotesovec, 28.2.2010):
explicit formula (first part) by Vaclav Kotesovec

explicit formula (first part) by Vaclav Kotesovec

(first part of formula in closed form)

A174154 - Number of ways to place 6n nonattacking kings on a 12 x 2n chessboard
Tento případ vyžadoval provést (na symbolické úrovni) inverzi matice velikosti 448 x 448, což je na hranici možností současných matematických programů (Derive6 ani Mathematica7 si s tím neporadí, na tyto velké matice je ale vhodný program Matlab7, který inverzi zvládl v čase 68 minut).
Vytvořující funkce (Generating function) (V. Kotesovec, 8.3.2010):

-x*(9881265328704000000x^74-745460194573987200000x^73 +27058441331237911560000x^72-630574519733958189096000x^71 +10620992412418133969628300x^70-137991665381256761637404520x^69 +1441187713449842720703280065x^68-12449684907187405839719194626x^67 +90833482252388172827285029638x^66-568749753878989316529701677248x^65 +3094959104534048177533681352799x^64-14786591491557537432688402148814x^63 +62546683770100863224056803287942x^62-235893075161001219428756666935555x^61 +797978924681191303527565813197295x^60-2433648791133257840409309484158509x^59 +6721172925589000338821415074614101x^58-16874983210908760792785651385114152x^57 +38649671515505567165916997301106375x^56-80999469039951794157868014640691605x^55 +155756628296635763280353356415757902x^54-275499172743267856241417580914101161x^53 +449253470876074605154885582765085506x^52-676816476591070935766817355948817667x^51 +943857986354193371364615928444017845x^50-1220661704439047432548206117121008699x^49 +1466533837456537613456821872852081734x^48-1639525223616587182652341410467569787x^47 +1708305101435402614973823579541075741x^46-1661495320924220763537985553529107570x^45 +1510621894675464930498400295672730343x^44-1285696520181304471064162857556756892x^43 +1025670064685839353596509770775335305x^42-767836201105618743331897589888819260x^41 +539952432414375273203309417443882230x^40-356956219188072917117313500791428647x^39 +221967416303673380170960689222016760x^38-129868144295605689997008303392471184x^37 +71491160008257450681327802590567504x^36-37017322185220125774414395796648083x^35 +18017697561193232235536013176700652x^34-8236705210457078339411642367777062x^33 +3532451891465875904778828049906178x^32-1419311438083676683034744726952652x^31 +533432327695298858210381553149285x^30-187205875643334525147970829585222x^29 +61228416399158699804621484828993x^28-18622737469829899757436340257385x^27 +5254673072129348277153109543997x^26-1371752804262578223890375168964x^25 +330267098353842775956388942842x^24-73061510988747055309122504069x^23 +14782596349429679171765334301x^22-2719571348796162565504741678x^21 +451339375837487448675798746x^20-66805240600688222182861662x^19 +8661523087250332029653805x^18-952009254666126966673796x^17 +82335998894700394651901x^16-4266725433179907174031x^15-184755253316270694616x^14 +83877913428258704659x^13-13092670253017397215x^12 +1433917521601031600x^11-120787644461247815x^10 +7805125834561750x^9-355282797168619x^8 +7110673719021x^7 +486018670449x^6-61151293377x^5 +3632842475x^4-141485072x^3 +3689608x^2-59281x+448) /(x-1)/(2x-1)/(4x-1)/(7x-1)^2/(x^2-3x+1)/(2x^2-5x+1)/(3x^2-5x+1)/(3x^2-6x+1)/(5x^2-7x+1)^2/(8x^2-7x+1)^2/(9x^2-7x+1)^3/(11x^2-7x+1)^2/(x^3-9x^2+6x-1)/(3x^3-11x^2+7x-1)^2/(3x^3-12x^2+7x-1)^2/(4x^3-11x^2+7x-1)/(5x^3-12x^2+7x-1)^2/(5x^3-13x^2+7x-1)^2/(7x^3-14x^2+7x-1)^2/(x^4-7x^3+13x^2-7x+1)/(x^4-8x^3+14x^2-7x+1)

Rekurentní vzorec:
a_n = 200a_n-1 -19591a_n-2 +1252845a_n-3 -58827505a_n-4 +2162753808a_n-5 -64829889078a_n-6 +1629240689182a_n-7 -35031124501133a_n-8 +654454967945240a_n-9 -10752566037209576a_n-10 +156879699829988516a_n-11 -2048776097631017397a_n-12 +24108171056426689513a_n-13 -257034531080309116618a_n-14 +2494772567482865677279a_n-15 -22133280277582878693605a_n-16 +180118887001001382183984a_n-17 -1348636789867805112026274a_n-18 +9315545713899467284553179a_n-19 -59499168382845285726017972a_n-20 +352120178477097682063693543a_n-21 -1934323013107671509059832463a_n-22 +9878966314646961189006272617a_n-23 -46972249732573258020377866081a_n-24 +208183877121467820793024020729a_n-25 -860974589150724576064816096663a_n-26 +3325616222441474827288188284748a_n-27 -12007102646405027060206035093213a_n-28 +40549313398041902425202637254740a_n-29 -128160961960827405525713512244418a_n-30 +379279006512370536257299017344107a_n-31 -1051368905565268405109177617606550a_n-32 +2730662700682795572522784530198834a_n-33 -6646355208785503282827723317955069a_n-34 +15161829507999599355831555503563964a_n-35 -32418089419841604310504626066285593a_n-36 +64963905091650869917279263108816530a_n-37 -121998193028385383238635351043687855a_n-38 +214657313735486368434302654748877496a_n-39 -353777524153903526644871915284150291a_n-40 +545952447651523245976395515654219577a_n-41 -788557229845726031285071277862716138a_n-42 +1065477899782050092815249173889044974a_n-43 -1345958367592910697332763314344919726a_n-44 +1588548886423131006699445390007535964a_n-45 -1750322460004952351721691789849070497a_n-46 +1798910520031476972425563369104737493a_n-47 -1722886523923952992401312780338774274a_n-48 +1536009690078173688532095945663171041a_n-49 -1273224933191855545781650218877302946a_n-50 +979983174726292730062221357725344727a_n-51 -699362171154778642087707164485332698a_n-52 +462015283859449079185102433429700638a_n-53 -282037700090254407809166846000612848a_n-54 +158780300135911015654982957271875917a_n-55 -82256781284683621993873503316293537a_n-56 +39117488543991922262702977386610326a_n-57 -17029736085111484438301715527001011a_n-58 +6766292666982799092814924628874630a_n-59 -2445102358065760086073498440897006a_n-60 +800463457818116640733412431607635a_n-61 -236339003295391504639451351871623a_n-62 +62608507068414191797382321464409a_n-63 -14791881602747947642116948625728a_n-64 +3094801634963547035936901282789a_n-65 -568588000125534978580839232812a_n-66 +90798410660368398860732240817a_n-67 -12444769805881872152497521690a_n-68 +1440691704088085224964754909a_n-69 -137955444475738809516914520a_n-70 +10619160418237292545913100a_n-71 -630516845227291857576000a_n-72 +27057588402917527560000a_n-73 -745460194573987200000a_n-74 +9881265328704000000a_n-75, n>75

Explicitní vzorec (numericky) (V. Kotesovec, 9.3.2010):
f6(n) = ("c1"*n+"c2")*7ⁿ
+"c3"*4ⁿ
+"c4"*2ⁿ
+"c5"
+("c6"*n^2+"c7"*n+"c8")*(SQRT(13)/2+7/2)ⁿ
+("c9"*n^2+"c10"*n+"c11")*(7/2-SQRT(13)/2)ⁿ
+("c12"*n+"c13")*(SQRT(29)/2+7/2)ⁿ
+("c14"*n+"c15")*(7/2-SQRT(29)/2)ⁿ
+("c16"*n+"c17")*(SQRT(17)/2+7/2)ⁿ
+("c18"*n+"c19")*(7/2-SQRT(17)/2)ⁿ
+("c20"*n+"c21")*(SQRT(5)/2+7/2)ⁿ
+("c22"*n+"c23")*(7/2-SQRT(5)/2)ⁿ
+"c24"*(SQRT(5)/2+3/2)ⁿ
+"c25"*(3/2-SQRT(5)/2)ⁿ
+"c26"*(SQRT(17)/2+5/2)ⁿ
+"c27"*(5/2-SQRT(17)/2)ⁿ
+"c28"*(SQRT(13)/2+5/2)ⁿ
+"c29"*(5/2-SQRT(13)/2)ⁿ
+"c30"*(SQRT(6)+3)ⁿ
+"c31"*(3-SQRT(6))ⁿ
+("c32"*n+"c33")*(9/(11-2*SQRT(58)*COS(ATAN(9*SQRT(303)/413)/3+pi/3)))ⁿ
+("c34"*n+"c35")*(9/(11-2*SQRT(58)*SIN(ACOT(-9*SQRT(303)/413)/3)))ⁿ
+("c36"*n+"c37")*(9/(2*SQRT(58)*COS(ATAN(9*SQRT(303)/413)/3)+11))ⁿ
+("c38"*n+"c39")*(3/(2*(2-3*COS(2*ACOT(-SQRT(107)/107)/3))))ⁿ
+("c40"*n+"c41")*(3/(2*(2-3*SIN(2*ATAN(SQRT(107)/107)/3+pi/6))))ⁿ
+("c42"*n+"c43")*(3/(2*(3*COS(2*ATAN(SQRT(107)/107)/3)+2)))ⁿ
+("c44"*n+"c45")*(5*SQRT(3)/(2*(2*SQRT(3)-SQRT(13)*COS(ATAN(5*SQRT(3)/9)/3+pi/3))))ⁿ
+("c46"*n+"c47")*(5*SQRT(3)/(2*(2*SQRT(3)-SQRT(13)*SIN(ACOT(-5*SQRT(3)/9)/3))))ⁿ
+("c48"*n+"c49")*(5*SQRT(3)/(2*(SQRT(13)*COS(ATAN(5*SQRT(3)/9)/3)+2*SQRT(3))))ⁿ
+("c50"*n+"c51")*(15/(13-16*COS(2*ACOT(-5*SQRT(111)/333)/3)))ⁿ
+("c52"*n+"c53")*(15/(13-16*SIN(2*ATAN(5*SQRT(111)/333)/3+pi/6)))ⁿ
+("c54"*n+"c55")*(15/(16*COS(2*ATAN(5*SQRT(111)/333)/3)+13))ⁿ
+("c56"*n+"c57")*(3/(2*(1-COS(2*ACOT(-SQRT(3)/9)/3))))ⁿ
+("c58"*n+"c59")*(3/(2*(1-SIN(2*ATAN(SQRT(3)/9)/3+pi/6))))ⁿ
+("c60"*n+"c61")*(3/(2*(COS(2*ATAN(SQRT(3)/9)/3)+1)))ⁿ
+"c62"*(1/(3-2*SQRT(7)*COS(ATAN(SQRT(3)/37)/3+pi/3)))ⁿ
+"c63"*(1/(3-2*SQRT(7)*SIN(ACOT(-SQRT(3)/37)/3)))ⁿ
+"c64"*(1/(2*SQRT(7)*COS(ATAN(SQRT(3)/37)/3)+3))ⁿ
+"c65"*(12/(11-2*SQRT(37)*COS(ATAN(6*SQRT(687)/161)/3+pi/3)))ⁿ
+"c66"*(12/(11-2*SQRT(37)*SIN(ACOT(-6*SQRT(687)/161)/3)))ⁿ
+"c67"*(12/(2*SQRT(37)*COS(ATAN(6*SQRT(687)/161)/3)+11))ⁿ
+"c68"*(SQRT(38-14*SQRT(5))/4-SQRT(5)/4+7/4)ⁿ
+"c69"*(-SQRT(38-14*SQRT(5))/4-SQRT(5)/4+7/4)ⁿ
+"c70"*(SQRT(14*SQRT(5)+38)/4+SQRT(5)/4+7/4)ⁿ
+"c71"*(-SQRT(14*SQRT(5)+38)/4+SQRT(5)/4+7/4)ⁿ
+"c72"*(SQRT(6*SQRT(5)+30)/4+SQRT(5)/4+7/4)ⁿ
+"c73"*(-SQRT(6*SQRT(5)+30)/4+SQRT(5)/4+7/4)ⁿ
+"c74"*(SQRT(30-6*SQRT(5))/4-SQRT(5)/4+7/4)ⁿ
+"c75"*(-SQRT(30-6*SQRT(5))/4-SQRT(5)/4+7/4)ⁿ

Z konstant c1 až c75 je nejzajímavější konstanta c1 u členu s nejvyšší váhou, viz též tabulka dále
"c1"=5.6305092363081393300...*10^5
"c2"=-1.104167141369220611...*10^7
"c3"=-2.357744324111866969...*10^6
"c4"=21.0432
"c5"=0.4722222222222222222...
"c6"=3190.3093489289550735...
"c7"=3.3724816112053204772...*10^5
"c8"=2.2171312563933296610...*10^7
"c9"=-0.155502775108919675...
"c10"=163.7653409000415659...
"c11"=2.052693391056922234...*10^4
"c12"=5.758468547897144015...*10^5
"c13"=1.624760528438350563...*10^7
"c14"=0.001165834594259474...
"c15"=-0.41441832002393772...
"c16"=2.300478493334472119...*10^5
"c17"=-1.44639696705190542...*10^7
"c18"=0.338908296854086023...
"c19"=8.005890335704876443...
"c20"=-4380.77992117273774...
"c21"=1.552146086172787699...*10^7
"c22"=74.67426089779847392...
"c23"=-4.21203713796980065...*10^4
"c24"=-1466.89599084080095...
"c25"=3.191774075165802562...*10^(-5)
"c26"=-1.36341829271227595...*10^6
"c27"=0.053980304804581505...
"c28"=7.075976996099561648...*10^4
"c29"=-0.02122530224411394...
"c30"=-1.46797239653638789...*10^7
"c31"=0.098837563176994140...
"c32"=0.011468815268292507...
"c33"=-34.8712694667255141...
"c34"=-2931.17833825432167...
"c35"=2.359570457373671675...*10^6
"c36"=-0.01023220098644473...
"c37"=-0.00976071273489356...
"c38"=79.63702226259701650...
"c39"=7623.522283711869170...
"c40"=-2.50405135693327250...*10^4
"c41"=-4.37105580792831970...*10^6
"c42"=-0.00017645871779939...
"c43"=-0.01873137641764468...
"c44"=182.8430686773159592...
"c45"=-2.05091907645515941...*10^4
"c46"=4.369015291089355051...*10^4
"c47"=-8.98717155512840790...*10^6
"c48"=0.030434481624558909...
"c49"=0.091021909918317851...
"c50"=81.04059263702932797...
"c51"=1.249689694089438109...*10^4
"c52"=6218.228392475138846...
"c53"=4.152739581799171110...*10^5
"c54"=-0.00911244704526967...
"c55"=0.070667837190544279...
"c56"=-277.104247927338245...
"c57"=2.816445813687916256...*10^4
"c58"=-2410.10041406045040...
"c59"=1.906847363789349701...*10^5
"c60"=-6.04826431426482591...*10^(-5)
"c61"=-0.03986068056420358...
"c62"=-1145.44167952134069...
"c63"=5.746421629805880771...*10^4
"c64"=-1.27578541046112266...*10^(-5)
"c65"=2.716923048103320883...
"c66"=-1.24844204776308025...*10^6
"c67"=-0.02476586191937392...
"c68"=-9.69121675380289883...
"c69"=0.002234055238103441...
"c70"=3.227848424788018850...*10^4
"c71"=-0.01279090254065370...
"c72"=1.446790521731934022...*10^6
"c73"=-0.17181958108958812...
"c74"=-3559.96835962473958...
"c75"=0.000767722202736206...

A174155 - Number of ways to place 7n nonattacking kings on a 14 x 2n chessboard
Tento případ vyžadoval pro získání vytvořující funkce provést (na symbolické úrovni!) inverzi matice velikosti 1024 x 1024, což ze současných matematických programů na PC zvládl pouze Matlab7 v čase přes 8 hodin.
Vytvořující funkce (Generating function) (V. Kotesovec, 9.3.2010):

-2x(54222672911274911289059573760000000x^123-6279364401720347209864467972096000000x^122 +355916700860805743977756391154647040000x^121-13165656678159747994229085738759094272000x^120 +357580968786334728976290764494328561664000x^119-7606685500377828944402424153754395444510720x^118 +132025070498240400453821981247031745011777536x^117-1923148717983096485894432339969762419764363264x^116 +24001598451495916558037784079325597030940672000x^115-260733912714136996693533608123205367579054964736x^114 +2496313284158021796255065102282597952375849222144x^113-21277865832851787547991827395328601974018991456256x^112 +162819416994113682338598213096466301319887512928256x^111-1126358581030907656491986254406033294612551232913408x^110 +7086514400960731390328723893313619097901288581496832x^109-40757758341169693402147178689047453376348442921533440x^108 +215257037478349801305513176871426454908220485492801536x^107-1048058512243529559822666262068066405115673243213627392x^106 +4720742792928429097850271439387849238995832815146369024x^105-19732519791798674006897568748598939801049082241955069952x^104 +76756113443806605398650302720172795659712890994488901632x^103-278543117088434677065138311184638719760885595939909009408x^102 +945165490091678324412551307244000361076544393234133614592x^101-3005076664126071245872244757805376845758973901952126877696x^100 +8969167160819063116493944158832282378058214481923144220672x^99-25173494362748757456491747023570336965099474666885947408384x^98 +66544578438810679866701792371902931683947858391489794482176x^97-165915150472108230394017571109190057361624463233617396158464x^96 +390695976354665890074513984612903966800905181381260806209536x^95-869962058942296909688656575338098822622973290164727090757632x^94 +1833820369440762614157730722855821504244851903462283741575168x^93-3663162558208576997437411808620528134488856302642268009722880x^92 +6940816834168452591527174228257133363210122586267517300846592x^91-12485300731198250918868702608084089861324343287261785436221440x^90 +21338793564228109772500185812748834074577991696545058663716864x^89-34677121465423066397628237863087661065799673463314127032121856x^88 +53618151940174275326509797819558207050312413538008687145720320x^87-78930471903810521140079827741654338728936679603061202109775616x^86 +110684484068511808086435721720485932701236358427760746915584128x^85-147931694677541828719396650661604635971538787804520097489430720x^84 +188525824622441412447766259940603893941456175662333549010704640x^83-229191721343564863372095426973769973171257827414431011627276224x^82 +265895245461053857121393536010031648750961599245321451639861696x^81-294478601111715286464524887097776472383327199903667055093108064x^80 +311429881070928442091929664868298832042011215780888541843889024x^79-314591478165462374119104556767298517772413598384303253181601680x^78 +303610313847801927302628453791220291803390622403746890286002928x^77-280000546810486798955803689372202305079421577088215075049437392x^76 +246804103133939308093322655758451920966947006188480655154502768x^75-207953075119753681934511769916178379442671053267567217312801856x^74 +167516671923783503099492383592992508412397913200612862784395728x^73-129028318635429191186157503073887054868563348499260954458336584x^72 +95038266464215381821909442668919890469926733009931919704337376x^71-66950284625201671155069063428880073031737512053977063096825228x^70 +45113692375805864259297990894062359371832009035289711397936572x^69-29083271562407026217147121592147394606754705984695471985211124x^68 +17941543124532772358042257555368380493701702794985559340294296x^67-10594988086421513826949788846676673068705561304545158471667176x^66 +5991920401275728684972283544592363416138938055314116591319068x^65-3247426373656460046505919451533942542620882729601342871800392x^64 +1688165453584027719109749622892479797351061811465406015315584x^63-842820130777935012431294163831220960459990279182114470001058x^62 +404786291367071435200584329565320034572896308441820233742492x^61-187427652608776303903657214006392302066849785191588678445115x^60 +83896074599720207110842887078480982574996945714857399371613x^59-36421099514154882084087090198951010669125624752881141912710x^58 +15389237595338812516875007712544226815442894222052921181201x^57-6351568145491846549236967852474091662341017080740623603308x^56 +2568470735966551607363059267449023563857322215129129292009x^55-1019698617782603122804098776612193889543052048554602751427x^54 +397651156321907497202559006733450549773666880896232550657x^53-152155733575897092189571737592541028133454734267411181214x^52 +56981485495617844103050419523305702033850394150958337929x^51-20812575067663039288298005399000342062645182032314841804x^50 +7385399296884771556614272143326975515992615453424039706x^49-2536378970991959824151513109283300166684452996715135613x^48 +840120945435246927097038897868232751926844215337475933x^47-267592212832787322394881575729138879628424476161213860x^46 +81762553246257166816899290032251339568459510030642883x^45-23918585500218748129692083027726169290403007263721516x^44 +6688609148248353532236759219142184861585117521757998x^43-1785680002635931884417620662660932079655295846414621x^42 +454652885121393630298466575461039200141902454472294x^41-110298017418873798104313766968125280060424724687194x^40 +25474543483790572391832217810646566581743665805776x^39-5596951496464420802889764068394845225964455321014x^38 +1168846911565928114777696452748844131217296980641x^37-231826928991979522819676069949495409863663665362x^36 +43629602459789761964817967344186988839256111996x^35-7783590869696391606863804898013090431960663692x^34 +1314850860746222381862072936753225528249707603x^33-210047845174210030771347734473617776144382113x^32 +31685847252072174706283091894572485340220424x^31-4505742353308488104812488551253836156494412x^30 +602733132978025015539972306763269356694723x^29-75657550530238560567564832465918129450573x^28 +8883682779620708497014362847653861413872x^27-971875320372166677407922243420697610663x^26 +98534825191761089609265874805355318687x^25-9189253210485381832768469226798168077x^24 +779442384966136549958627866012748423x^23-59012906619949767531288773139867455x^22 +3845953582977736963079436642919696x^21-197099229113974036917550559274814x^20 +5292802547783405050936604984656x^19 +373035447202117049725952469283x^18-77596506283090099467584030538x^17 +8167182777939867059910623158x^16-661371544219142909103681829x^15 +44836253686866816392727278x^14-2615582192513759386391326x^13 +132326561350181298705400x^12-5789711318908782442591x^11 +216507299180594552002x^10-6754590417985251086x^9 +167279960378322251x^8-2883766637590816x^7 +15171573646232x^6 +1034726376990x^5-43935972146x^4 +988301639x^3-14215547x^2 +124457x-512) /(x-1)/(2x-1)^4/(3x-1)/(4x-1)^2/(5x-1)^2/(6x-1)^2/(8x-1)^2/(x^2-3x+1)/(2x^2-5x+1)/(2x^2-6x+1)^2/(3x^2-5x+1)/(3x^2-6x+1)/(4x^2-6x+1)/(5x^2-5x+1)/(4x^2-7x+1)/(6x^2-6x+1)/(6x^2-8x+1)^2/(x^3-5x^2+6x-1)^2/(10x^2-8x+1)^2/(11x^2-8x+1)^2/(14x^2-8x+1)^2/(2x^3-12x^2+7x-1)/(3x^3-12x^2+7x-1)/(4x^3-15x^2+8x-1)^2/(6x^3-14x^2+8x-1)/(7x^3-15x^2+8x-1)^2/(6x^3-16x^2+8x-1)/(7x^3-17x^2+8x-1)/(8x^3-17x^2+8x-1)^2/(9x^3-17x^2+8x-1)/(10x^3-18x^2+8x-1)^2/(13x^3-19x^2+8x-1)^2/(2x^4-12x^3+18x^2-8x+1)/(2x^4-13x^3+19x^2-8x+1)/(2x^4-16x^3+20x^2-8x+1)/(3x^4-17x^3+20x^2-8x+1)^2

Rekurentní vzorec:
a_n = 355*a_n-1 -62230*a_n-2 +7181407*a_n-3 -613713773*a_n-4 +41424053008*a_n-5 -2300132364916*a_n-6 +108057442428713*a_n-7 -4383953038266400*a_n-8 +156019190373932213*a_n-9 -4931027930452931529*a_n-10 +139784688779506280122*a_n-11 -3583425170015054558692*a_n-12 +83642898320877743078649*a_n-13 -1788040425415361381095757*a_n-14 +35181295448283382870926529*a_n-15 -639901931020563711201074856*a_n-16 +10800089806681857038851260471*a_n-17 -169708489277667670527670553256*a_n-18 +2490164949669281400008934703650*a_n-19 -34209628251326791851770501894019*a_n-20 +441055288914550947143816216610085*a_n-21 -5347966902979544937526517923821060*a_n-22 +61104504039422023705912415093725325*a_n-23 -659032554611721554539403323301392328*a_n-24 +6720192949816044716232213169179554002*a_n-25 -64882805116093293907803507888980509652*a_n-26 +593920909802707572074736203520468111015*a_n-27 -5160703522797399132569345666788973860423*a_n-28 +42614522062811899586385927814456985353588*a_n-29 -334751895136451803946683064352275034359880*a_n-30 +2503907651659320142301076243661317011090301*a_n-31 -17849439080689433456741551238042933830148067*a_n-32 +121365103409983215634920731453706282402989836*a_n-33 -787682779457226999619540178398463725925966321*a_n-34 +4883125137114593719681433214140387829336583657*a_n-35 -28934196085932348822191609052145794097781155747*a_n-36 +163964259705601110511077019136782444452849185661*a_n-37 -889096467412574593575239829002444819262058789807*a_n-38 +4615620894756910152737471910113313680781105674422*a_n-39 -22950686917289066656110074511663942441885518753279*a_n-40 +109353457449972177331586073421680895966478823429493*a_n-41 -499473845738617512362949924094821709360026608128519*a_n-42 +2187734208783093331582990536307413775611383675314889*a_n-43 -9192273270269162035986926653043968654354343390001452*a_n-44 +37062129853043426095583096259451935804785975760076180*a_n-45 -143429198013863760183212109243115977359657995206014227*a_n-46 +532910058542910360324809278690568941113219846288868695*a_n-47 -1901420003705947087451752388740956303649285577893915347*a_n-48 +6516259041007093187423911613159101666641521933740754935*a_n-49 -21453256766715010406989098549201236384005949789118270289*a_n-50 +67862786677741974361372613468176344308979904185438584928*a_n-51 -206287780166253696570479597934268784316357437236102282981*a_n-52 +602656132334901791636594053942094239035756172510172525310*a_n-53 -1692241022898939503382665894593801620298884560230139707283*a_n-54 +4567571300316866260600043539420748909209366452509778579458*a_n-55 -11851263906173524614222522185343043279355263254029721988325*a_n-56 +29560920816547403978712649385739724088334537984011638988104*a_n-57 -70885121592790538286371080849899812856102357608828148982550*a_n-58 +163409845886211665485225388293159123346245205917080382491840*a_n-59 -362144494413274527626611628277027555974388120349867198704581*a_n-60 +771530456662294571647577757578775733382830746682477159631731*a_n-61 -1580051625970196573554375464352132643295757350774681162296206*a_n-62 +3110344753414776505140966019872337750496742905447614669866357*a_n-63 -5884768996639161507183480452281609414662222317037902572633129*a_n-64 +10700179904680098088349075595592950436046826427104304058777483*a_n-65 -18695761252218017203250136160781026224722427604030963411998550*a_n-66 +31385405428525582416952099102249644055680352511497855444441476*a_n-67 -50615010790428312789203366621293543617322532762055840704862044*a_n-68 +78401558190254541965541051943975685100181865096298253483692092*a_n-69 -116622609345361161550023273188650530719539499699634509198995280*a_n-70 +166557601271060887009843251325454304196590177972454959487144760*a_n-71 -228335053227695446593478422394263084067454263715584326278101612*a_n-72 +300401134446235301923820488428752926620010702980973240412254612*a_n-73 -379172847928243557624031458518329813721595270573144703516684576*a_n-74 +459046365839494135368978124958612394249433642265385081445950840*a_n-75 -532877482801746654124759269331287007133286813299814163092009072*a_n-76 +592936288102825622570743054492822496446897568699254213904468288*a_n-77 -632189153956996372446346209656511806473856827439391888927649744*a_n-78 +645628423168981359720232716143742154313424331606125466445192864*a_n-79 -631309538761675057717669169185910680560650899421336897795392864*a_n-80 +590802676516296103915411991460869361161536968482988725264860832*a_n-81 -528916884144943614094532055306563532933002357635647591545000256*a_n-82 +452761330701536545738119403023868339767065670518026635649577216*a_n-83 -370396653643622694057710469713707973757641810265926750337440128*a_n-84 +289431372618931391691737286015520606075875385437288774637611200*a_n-85 -215901264737140413666379352994934014775706019543589604786418560*a_n-86 +153649184549497317041659318233838481245117719730140911980842240*a_n-87 -104252974521213676768278500477636643016220002666862316826451968*a_n-88 +67395262889890487766296108102457389362138367464841581743008512*a_n-89 -41479473052975102408788350419058391326160347231275485649925632*a_n-90 +24286188570788191214124029153817764477465967752785084937249792*a_n-91 -13515885727784925849780266435732478478996532916115183858167808*a_n-92 +7143333320685061147938100094247033962091553666292792325552128*a_n-93 -3581905682072239982948980939843555015656793558885050106626048*a_n-94 +1702317826959975854072534402257549818094193265958637078077440*a_n-95 -765957974206249466198973766920615027158143875426684125339648*a_n-96 +325909060539351950294732186971109628679383105292872432025600*a_n-97 -130968165237993448475954170153250150473368153400646612811776*a_n-98 +49638708587887646409930310401068700758344054841911497785344*a_n-99 -17718229431449535703068175428258919870114054679778329591808*a_n-100 +5946636096612490129643987484131994525326081419538641305600*a_n-101 -1873351971906088407360195136745415764386870573863249346560*a_n-102 +552894140752297793897292472024667959143300503946233315328*a_n-103 -152559503760719436568492942301761635184890139055040757760*a_n-104 +39266537394375534967337770724827049041421713702333644800*a_n-105 -9403752773974119645286336014440818139548381446587940864*a_n-106 +2089612061057417202959800881701216993734109316216258560*a_n-107 -429504625481757418108462149946734473479836376897683456*a_n-108 +81375891864330772617336465883953945682230569494118400*a_n-109 -14156048922012863746909064485322036645034360708268032*a_n-110 +2250938891663231625620683440919224267817994365698048*a_n-111 -325484106592219042324298551387653940779270480592896*a_n-112 +42545385782902596634984070466084992703612208545792*a_n-113 -4992222373149232005879478421404380031384037621760*a_n-114 +521480049046471863976707137480219684646980419584*a_n-115 -48007121237350102099540488235719546567483457536*a_n-116 +3846701159492393552477177944898029698982871040*a_n-117 -264077394388027999670576258659387821659258880*a_n-118 +15214673796528838502205187025491559920435200*a_n-119 -715205037525577948424201523247561310208000*a_n-120 +26332207845103672186115068739494871040000*a_n-121 -711842230613175571260114828735283200000*a_n-122 +12558728803440694419728935944192000000*a_n-123 -108445345822549822578119147520000000*a_n-124, n>124

Explicitní vzorec (numericky) (V. Kotesovec, 10.3.2010):
f7(n) = ("c1"*n+"c2")*8ⁿ
+("c3"*n+"c4")*6ⁿ
+("c5"*n+"c6")*5ⁿ
+("c7"*n+"c8")*4ⁿ
+"c9"*3ⁿ
+("c10"*n^3+"c11"*n^2+"c12"*n+"c13")*2ⁿ
+"c14"
+("c15"*n+"c16")*(SQRT(7)+3)ⁿ
+("c17"*n+"c18")*(3-SQRT(7))ⁿ
+("c19"*n+"c20")*(SQRT(10)+4)ⁿ
+("c21"*n+"c22")*(4-SQRT(10))ⁿ
+("c23"*n+"c24")*(SQRT(6)+4)ⁿ
+("c25"*n+"c26")*(4-SQRT(6))ⁿ
+("c27"*n+"c28")*(SQRT(5)+4)ⁿ
+("c29"*n+"c30")*(4-SQRT(5))ⁿ
+("c31"*n+"c32")*(SQRT(2)+4)ⁿ
+("c33"*n+"c34")*(4-SQRT(2))ⁿ
+"c35"*(SQRT(5)/2+3/2)ⁿ
+"c36"*(3/2-SQRT(5)/2)ⁿ
+"c37"*(SQRT(17)/2+5/2)ⁿ
+"c38"*(5/2-SQRT(17)/2)ⁿ
+"c39"*(SQRT(13)/2+5/2)ⁿ
+"c40"*(5/2-SQRT(13)/2)ⁿ
+"c41"*(SQRT(6)+3)ⁿ
+"c42"*(3-SQRT(6))ⁿ
+"c43"*(SQRT(5)+3)ⁿ
+"c44"*(3-SQRT(5))ⁿ
+"c45"*(SQRT(5)/2+5/2)ⁿ
+"c46"*(5/2-SQRT(5)/2)ⁿ
+"c47"*(SQRT(33)/2+7/2)ⁿ
+"c48"*(7/2-SQRT(33)/2)ⁿ
+"c49"*(SQRT(3)+3)ⁿ
+"c50"*(3-SQRT(3))ⁿ
+("c51"*n+"c52")*(3/(5-2*SQRT(7)*COS(ACOT(-SQRT(3)/9)/3)))ⁿ
+("c53"*n+"c54")*(3/(2*SQRT(7)*SIN(ATAN(SQRT(3)/9)/3+pi/3)+5))ⁿ
+("c55"*n+"c56")*(3/(5-2*SQRT(7)*SIN(ATAN(SQRT(3)/9)/3)))ⁿ
+("c57"*n+"c58")*(4*SQRT(3)/(5*SQRT(3)-2*SQRT(43)*COS(ATAN(4*SQRT(687)/477)/3+pi/3)))ⁿ
+("c59"*n+"c60")*(4*SQRT(3)/(5*SQRT(3)-2*SQRT(43)*SIN(ACOT(-4*SQRT(687)/477)/3)))ⁿ
+("c61"*n+"c62")*(4*SQRT(3)/(2*SQRT(43)*COS(ATAN(4*SQRT(687)/477)/3)+5*SQRT(3)))ⁿ
+("c63"*n+"c64")*(7*SQRT(3)/(5*SQRT(3)-2*SQRT(19)*COS(ACOT(-3*SQRT(3)/7)/3)))ⁿ
+("c65"*n+"c66")*(7*SQRT(3)/(2*SQRT(19)*SIN(ATAN(3*SQRT(3)/7)/3+pi/3)+5*SQRT(3)))ⁿ
+("c67"*n+"c68")*(7*SQRT(3)/(5*SQRT(3)-2*SQRT(19)*SIN(ATAN(3*SQRT(3)/7)/3)))ⁿ
+("c69"*n+"c70")*(24/(17-2*SQRT(97)*COS(ATAN(24*SQRT(237)/881)/3+pi/3)))ⁿ
+("c71"*n+"c72")*(24/(17-2*SQRT(97)*SIN(ACOT(-24*SQRT(237)/881)/3)))ⁿ
+("c73"*n+"c74")*(24/(2*SQRT(97)*COS(ATAN(24*SQRT(237)/881)/3)+17))ⁿ
+("c75"*n+"c76")*(5*SQRT(3)/(3*SQRT(3)-2*SQRT(7)*COS(ATAN(5*SQRT(111)/117)/3+pi/3)))ⁿ
+("c77"*n+"c78")*(5*SQRT(3)/(3*SQRT(3)-2*SQRT(7)*SIN(ACOT(-5*SQRT(111)/117)/3)))ⁿ
+("c79"*n+"c80")*(5*SQRT(3)/(2*SQRT(7)*COS(ATAN(5*SQRT(111)/117)/3)+3*SQRT(3)))ⁿ
+("c81"*n+"c82")*(39/(19-14*COS(4*ATAN(SQRT(3)/9)/3+pi/3)))ⁿ
+("c83"*n+"c84")*(39/(19-14*SIN(4*ATAN(SQRT(3)/9)/3+pi/6)))ⁿ
+("c85"*n+"c86")*(39/(14*COS(4*ATAN(SQRT(3)/9)/3)+19))ⁿ
+"c87"*(SQRT(6)/(2*(SQRT(6)-SQRT(17)*COS(ATAN(SQRT(237)/171)/3+pi/3))))ⁿ
+"c88"*(SQRT(6)/(2*(SQRT(6)-SQRT(17)*SIN(ACOT(-SQRT(237)/171)/3))))ⁿ
+"c89"*(SQRT(6)/(2*(SQRT(17)*COS(ATAN(SQRT(237)/171)/3)+SQRT(6))))ⁿ
+"c90"*(3/(2*(2-3*COS(2*ACOT(-SQRT(107)/107)/3))))ⁿ
+"c91"*(3/(2*(2-3*SIN(2*ATAN(SQRT(107)/107)/3+pi/6))))ⁿ
+"c92"*(3/(2*(3*COS(2*ATAN(SQRT(107)/107)/3)+2)))ⁿ
+"c93"*(9/(7-2*SQRT(13)*COS(ACOT(-103*SQRT(303)/2727)/3)))ⁿ
+"c94"*(9/(2*SQRT(13)*SIN(ATAN(103*SQRT(303)/2727)/3+pi/3)+7))ⁿ
+"c95"*(9/(7-2*SQRT(13)*SIN(ATAN(103*SQRT(303)/2727)/3)))ⁿ
+"c96"*(9/(4*(2-SQRT(7)*COS(ATAN(27*SQRT(47)/563)/3+pi/3))))ⁿ
+"c97"*(9/(4*(2-SQRT(7)*SIN(ACOT(-27*SQRT(47)/563)/3))))ⁿ
+"c98"*(9/(4*(SQRT(7)*COS(ATAN(27*SQRT(47)/563)/3)+2)))ⁿ
+"c99"*(21/(17-22*COS(2*ACOT(-9*SQRT(107)/749)/3)))ⁿ
+"c100"*(21/(17-22*SIN(2*ATAN(9*SQRT(107)/749)/3+pi/6)))ⁿ
+"c101"*(21/(22*COS(2*ATAN(9*SQRT(107)/749)/3)+17))ⁿ
+"c102"*(27/(17-2*SQRT(73)*COS(ATAN(27*SQRT(771)/997)/3+pi/3)))ⁿ
+"c103"*(27/(17-2*SQRT(73)*SIN(ACOT(-27*SQRT(771)/997)/3)))ⁿ
+"c104"*(27/(2*SQRT(73)*COS(ATAN(27*SQRT(771)/997)/3)+17))ⁿ
+("c105"*n+"c106")*(-12/(SQRT(129-16*SQRT(7)*COS(ACOT(-187*SQRT(5871)/17613)/3))+SQRT(16*SQRT(7)*SIN(ATAN(187*SQRT(5871)/17613)/3+pi/3)+129)-SQRT(129-16*SQRT(7)*SIN(ATAN(187*SQRT(5871)/17613)/3))-17))ⁿ
+("c107"*n+"c108")*(-12/(SQRT(129-16*SQRT(7)*COS(ACOT(-187*SQRT(5871)/17613)/3))-SQRT(16*SQRT(7)*SIN(ATAN(187*SQRT(5871)/17613)/3+pi/3)+129)+SQRT(129-16*SQRT(7)*SIN(ATAN(187*SQRT(5871)/17613)/3))-17))ⁿ
+("c109"*n+"c110")*(12/(SQRT(129-16*SQRT(7)*COS(ACOT(-187*SQRT(5871)/17613)/3))-SQRT(16*SQRT(7)*SIN(ATAN(187*SQRT(5871)/17613)/3+pi/3)+129)-SQRT(129-16*SQRT(7)*SIN(ATAN(187*SQRT(5871)/17613)/3))+17))ⁿ
+("c111"*n+"c112")*(12/(SQRT(129-16*SQRT(7)*COS(ACOT(-187*SQRT(5871)/17613)/3))+SQRT(16*SQRT(7)*SIN(ATAN(187*SQRT(5871)/17613)/3+pi/3)+129)+SQRT(129-16*SQRT(7)*SIN(ATAN(187*SQRT(5871)/17613)/3))+17))ⁿ
+"c113"*(SQRT(4*SQRT(2)+10)/2+SQRT(2)/2+2)ⁿ
+"c114"*(-SQRT(4*SQRT(2)+10)/2+SQRT(2)/2+2)ⁿ
+"c115"*(SQRT(10-4*SQRT(2))/2-SQRT(2)/2+2)ⁿ
+"c116"*(-SQRT(10-4*SQRT(2))/2-SQRT(2)/2+2)ⁿ
+"c117"*(-8*SQRT(3)/(SQRT(203-16*SQRT(73)*COS(ATAN(3*SQRT(8331)/1217)/3+pi/3))+SQRT(203-16*SQRT(73)*SIN(ACOT(-3*SQRT(8331)/1217)/3))-SQRT(16*SQRT(73)*COS(ATAN(3*SQRT(8331)/1217)/3)+203)-13*SQRT(3)))ⁿ
+"c118"*(-8*SQRT(3)/(SQRT(203-16*SQRT(73)*COS(ATAN(3*SQRT(8331)/1217)/3+pi/3))-SQRT(203-16*SQRT(73)*SIN(ACOT(-3*SQRT(8331)/1217)/3))+SQRT(16*SQRT(73)*COS(ATAN(3*SQRT(8331)/1217)/3)+203)-13*SQRT(3)))ⁿ
+"c119"*(8*SQRT(3)/(SQRT(203-16*SQRT(73)*COS(ATAN(3*SQRT(8331)/1217)/3+pi/3))-SQRT(203-16*SQRT(73)*SIN(ACOT(-3*SQRT(8331)/1217)/3))-SQRT(16*SQRT(73)*COS(ATAN(3*SQRT(8331)/1217)/3)+203)+13*SQRT(3)))ⁿ
+"c120"*(8*SQRT(3)/(SQRT(203-16*SQRT(73)*COS(ATAN(3*SQRT(8331)/1217)/3+pi/3))+SQRT(203-16*SQRT(73)*SIN(ACOT(-3*SQRT(8331)/1217)/3))+SQRT(16*SQRT(73)*COS(ATAN(3*SQRT(8331)/1217)/3)+203)+13*SQRT(3)))ⁿ
+"c121"*(SQRT(2-SQRT(2))+2)ⁿ
+"c122"*(2-SQRT(2-SQRT(2)))ⁿ
+"c123"*(SQRT(SQRT(2)+2)+2)ⁿ
+"c124"*(2-SQRT(SQRT(2)+2))ⁿ

Zde musím znovu upozornit na různou implementaci funkce ArcCot v programu Mathematica7 (a shodně Matlab7) pro záporné argumenty. Podle tohoto programu vyjde např. ArcCot(-1)=-pi/4, zatímco Derive6 dává svou funkcí ACOT(-1)=3*pi/4. Pro kladné argumenty jsou výsledky totožné. Výše uvedený vzorec pracuje s interpretací ACOT.

"c1" = 8.008508288587027981899891832842...*10^6
"c2" = -1.81089995748716180171175024872...*10^8
"c3" = 4086940.5
"c4" = 2.713279915661047027506654835847...*10^8
"c5" = 811926.2319051077221011861534737...
"c6" = -1.31369302331806894332700374141...*10^8
"c7" = 18170.88
"c8" = -4.17999101238672438672438672438...*10^6
"c9" = -6228.83108571428571428571428571...
"c10" = 0.043738977072310405643738977072...
"c11" = 1.421557067271352985638699924414...
"c12" = -30.9432558998908205257411606617...
"c13" = -220.043520976456426191875927325...
"c14" = -5.86718496922578555231616456106...
"c15" = -418788.523607094712529342554505...
"c16" = 5.013707630801773104192477688378...*10^8
"c17" = -0.02492925229172231612073699179...
"c18" = 1.075364029453712760657536485049...
"c19" = 8.540270388258272352607112248837...*10^6
"c20" = 2.814350377821712904853391678413...*10^8
"c21" = 1.041333163798738377996052789276...
"c22" = -345.614397009437947019921430265...
"c23" = 1.324647893190896933017015071967...*10^7
"c24" = -9.73346177369950808833328888260...*10^8
"c25" = 1.628231381547022831736466874142...
"c26" = 66.98500631230045022769121311433...
"c27" = 2.461688914751622082783683674985...*10^7
"c28" = 8.426569154599938669036500370553...*10^8
"c29" = -3433.96380047215658028992763237...
"c30" = -879817.398340831956494809134168...
"c31" = -1.08277959139968522739644207730...*10^7
"c32" = -1.11370658910819897649267299049...*10^9
"c33" = -172912.835854753195647189481178...
"c34" = 1.724253902964595606877325046590...*10^7
"c35" = 72107.92221362639378910892248909...
"c36" = 0.419902292407003414221448250425...
"c37" = -8.11395447235995889385202278688...*10^6
"c38" = 0.018419861981117514634920814561...
"c39" = -1.01541967361319499179816518714...*10^7
"c40" = 0.668765201148772650662715793661...
"c41" = 2.308626082413440881556439274072...*10^9
"c42" = 1.744554864061056687088635412236...
"c43" = 8.206033292160349219251536757333...*10^6
"c44" = 0.109944913938643200084771315292...
"c45" = -385037.804303049272027195013717...
"c46" = 0.616428707628469127869660571766...
"c47" = -2.97399811196902055787451969786...*10^8
"c48" = -3.76849765053512829175687214279...
"c49" = -7.47216380568250569395536302955...*10^7
"c50" = 0.511428304931231374039374725970...
"c51" = 150738.8203858169019828385146415...
"c52" = -5.18824642004650146213559150392...*10^7
"c53" = -0.04451870042271629938786815225...
"c54" = -0.97177685106174796757718162692...
"c55" = 8.099024789246810243321779432971...
"c56" = 693.2457214795661483544460653979...
"c57" = -4849.79021955111715653639024285...
"c58" = -1.47268544573164061772075206359...*10^6
"c59" = -1.96873464171550841512243324289...*10^6
"c60" = -4.76180445236817173759036301713...*10^8
"c61" = 0.000044184748555657770987329876...
"c62" = -0.20916425493071292134244414069...
"c63" = 816616.4078745858843854181312695...
"c64" = -9.80660449239965542007095900209...*10^8
"c65" = 0.540719173758396061324902848868...
"c66" = -0.59125375316823196724737514491...
"c67" = -3592.42020892921114172992973799...
"c68" = 879957.3686633784806555529260785...
"c69" = -4952.53864665607197453048394527...
"c70" = 674174.7111370475527269617358608...
"c71" = 171415.1705115741663145562364573...
"c72" = 1.159879075216887004259128792089...*10^8
"c73" = 6.228894575576546050196855027376...
"c74" = -698.160829928694354683331412339...
"c75" = -27852.4037526076503861051686847...
"c76" = 1.750866020046519344704183669533...*10^6
"c77" = -107316.548751238334290285095491...
"c78" = 1.700036068814900126759084523105...*10^7
"c79" = 2.140556705635654663312406910040...
"c80" = 354.1446359049725509269272638600...
"c81" = -87502.0975293379311029534402413...
"c82" = -1.99097669599308099559897241304...*10^7
"c83" = 132811.7138629216765267725267322...
"c84" = 8.578295334185319271128247289640...*10^6
"c85" = 1.392883434473521545674052378508...
"c86" = 53.58861446176947274622220632354...
"c87" = 16099.37906282671383085207399636...
"c88" = 2.152950747383693795804808879121...*10^6
"c89" = -0.00863842484944510025519818691...
"c90" = 7775.413981671499525081277300107...
"c91" = 1.451226993119440000835137043482...*10^6
"c92" = -0.26714117358513685377893621605...
"c93" = -1.75372066726327368313061403810...*10^8
"c94" = 1.901644993615794344161544022622...
"c95" = -48.1080973139087033202367677395...
"c96" = 585105.8413288281531550457051346...
"c97" = 5.806336199362658824686762759793...*10^7
"c98" = -0.67302107263106564653088387790...
"c99" = 65729.17344085680201901804876663...
"c100" = -3.51421283567362680415284551317...*10^8
"c101" = -0.22095977210544169098051582936...
"c102" = 63806.84331577325805659666923283...
"c103" = 1.060674960621817083637236991780...*10^8
"c104" = -7.75572499836378041062265279038...
"c105" = -10990.5020942609060998549371647...
"c106" = 796664.5780846115765133747463153...
"c107" = 3.425535244229768667392356486178...
"c108" = -55.0827638151146581597279068191...
"c109" = 116339.6059632768281029847362073...
"c110" = 1.174182642106513753397109896870...*10^7
"c111" = 0.000115067472477431864327897940...
"c112" = 0.017174626194380625642751954060...
"c113" = 2.971646179887972534926221265784...*10^8
"c114" = 11.01012889052251677479594737182...
"c115" = 143189.9095428102115806939589428...
"c116" = 0.230170922802426304709897115210...
"c117" = -2.56586075319021143803520294878...
"c118" = -395912.481421705580918482229332...
"c119" = 14633.18010963546792895745481650...
"c120" = 0.002989002374954112674911320720...
"c121" = -43179.2433928682842768066552894...
"c122" = 0.107980606874322436416084820539...
"c123" = -1.45231903646507818317408952466...*10^6
"c124" = 0.000026638467036372604464378334...

Number of ways to place 8n nonattacking kings on a 16 x 2n chessboard
Na matici velikosti 2304 x 2304 nestačí (při 4GB RAM) ani Matlab7. Vypočetl jsem proto alespoň determinant této transformační matice. Ten určuje tvar jmenovatele vytvořující funkce, tzv. denominator, ze kterého pak vyplývá tvar explicitního řešení. Program Mathematica7 zvládl výpočet determinantu této obrovské matice ve skvělém čase 5 hodin 35 minut. Výsledkem je polynom 882 stupně, který má 208 různých kořenů.

Denominator: (-1+x)³⁰(-1+2x)⁸(-1+3x)³²(-1+4x)²(-1+5x)⁴(-1+6x)²(-1+9x)²(1-5x+x²)²(1-3x+x²)¹⁶(1-5x+2x²)⁴(1-6x+3x²)⁶(1-6x+4x²)⁴(1-8x+5x²)²(1-6x+6x²)⁸(1-9x+7x²)⁴(1-7x+7x²)⁴(1-6x+7x²)²(1-7x+8x²)²(1-9x+12x²)⁴(1-9x+13x²)⁴(1-9x+15x²)⁴(1-9x+16x²)²(1-9x+17x²)⁴(1-9x+19x²)⁴(-1+6x-8x²+x³)²(-1+6x-7x²+x³)⁸(-1+5x-6x²+x³)²(-1+6x-8x²+2x³)⁴(-1+6x-9x²+3x³)⁴(-1+8x-16x²+4x³)²(-1+8x-15x²+4x³)⁴(-1+9x-18x²+5x³)⁴(-1+9x-17x²+5x³)⁴(-1+8x-16x²+6x³)⁴(-1+8x-17x²+7x³)⁴(-1+9x-21x²+8x³)⁴(-1+9x-20x²+8x³)⁴(-1+9x-19x²+8x³)⁴(-1+9x-17x²+8x³)⁴(-1+9x-22x²+9x³)²(-1+9x-19x²+9x³)⁴(-1+9x-18x²+9x³)⁴(-1+9x-22x²+11x³)⁴(-1+9x-21x²+11x³)⁴(-1+9x-21x²+12x³)⁸(-1+9x-22x²+13x³)⁴(-1+9x-23x²+14x³)⁴(-1+9x-22x²+15x³)⁴(-1+9x-23x²+16x³)⁴(-1+9x-24x²+17x³)⁴(-1+9x-24x²+19x³)⁴(1-8x+18x²-9x³+x⁴)²(1-9x+24x²-20x³+3x⁴)⁴(1-9x+24x²-18x³+3x⁴)⁴(1-9x+23x²-17x³+3x⁴)⁴(1-9x+22x²-16x³+3x⁴)⁴(1-9x+21x²-15x³+3x⁴)⁴(1-9x+25x²-22x³+4x⁴)⁴(1-9x+24x²-21x³+4x⁴)⁴(1-9x+24x²-19x³+4x⁴)⁴(1-9x+22x²-17x³+4x⁴)²(1-9x+26x²-26x³+5x⁴)⁴(1-9x+25x²-24x³+5x⁴)⁴(1-9x+25x²-23x³+5x⁴)⁴(1-9x+24x²-22x³+5x⁴)⁴(1-9x+24x²-20x³+5x⁴)⁴(1-9x+26x²-26x³+7x⁴)⁴(1-9x+26x²-27x³+8x⁴)⁸(1-9x+26x²-28x³+9x⁴)²(1-9x+27x²-31x³+11x⁴)⁴(-1+9x-28x²+35x³-15x⁴+x⁵)²(-1+9x-27x²+31x³-12x⁴+x⁵)⁴
(V. Kotesovec, 2.3.2010)

Zajímavé by bylo odvodit, jak se funkce f_m(n) chová pokud jde n do nekonečna. Z předchozích vzorců jde odhadnout tvar hlavního členu
f_m(n) ~ k_m*n*(m+1)ⁿ, hodnota "k" ale není konstanta, ale funkce závislá na "m".

m	k_m	k_m/k_m-1
1	1.00000
2	17.00000	17.00000
3	231.00000	13.58823
4	3051.17509	13.20855
5	40881.99638	13.39877
6	563050.92363	13.77258
7	8008508.28858	14.22341
8	?	?

Máme zatím velmi málo výsledků pro nějaký serióznější odhad. Mám ale hypotézu, že podíl k_m/k_m-1 konverguje k nějaké konstantě.

Převrácené hodnoty kořenů určují tvar partikulárních řešení. Pokud tyto hodnoty srovnáme podle velikosti, dostaneme následující tabulku a graf (pro m=1 až m=7). Jak již teoreticky dokázal ve svém článku The Problem of the Kings H. Wilf, člen s nejvyšší váhou má vždy hodnotu m+1, což jsem nyní potvrdil výpočty až do m=8.

r₁ = m + 1

Je však třeba poznamenat, že výpočet čísla druhého v pořadí, uvedený na konci citovaného článku, je chybný!
Formula for latter value in article by Wilf (1995) is wrong.
Right formula is (V. Kotesovec, 27.2.2010):

r₂ =

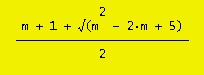(for m>1)

Dalším (poněkud překvapujícím) výsledkem je, že pro m jdoucí do nekonečna se první dvě největší čísla nevzdálí více jak o 1, přesněji

lim r₁ - r₂ = 1
m ® Ą

(V. Kotesovec, 27.2.2010)

root number	m=1	m=2	m=3	m=4	m=5	m=6	m=7	generally
1	2	3	4	5	6	7	8	m+1
2		2.618033988 3/2+sqrt(5)/2	3.414213562 2+sqrt(2)	4.302775637 5/2+sqrt(13)/2	5.236067977 3+sqrt(5)	6.192582403 7/2+sqrt(29)/2	7.16227766 4+sqrt(10)	(m+1 + sqrt(m²-2m+5))/2
3		0.381966011	3	4	4.732050807	5.561552812	6.449489742
4			0.585786437	3.732050807	4.561552812	5.449489742	6.372281323
5				3.618033988	4.414213562	5.302775637	6.236067977
6				3.246979603	4.214319743	4.935432331	6
7				1.554958132	4	4.866198262	5.744826077
8				1.381966011	3.879385241	4.651093408	5.645751311
9				1	3.732050807	4.618033988	5.507018644
10				0.697224362	3.414213562	4.561552812	5.449489742
11				0.267949192	2	4.460504870	5.414213562
12				0.198062264	1.652703644	4.390256884	5.323404276
13					1.585786437	4.302775637	5.236067977
14					1.460811128	4.170086486	5.086130197
15					1.267949192	4	5.048917339
16					0.763932022	3.956295201	5
17					0.585786437	3.801937735	4.912229178
18					0.467911113	3.532088886	4.813606502
19					0.438447187	2.618033988	4.732050807
20					0.324869128	2.445041868	4.699628148
21					0.267949192	2.381966011	4.685543932
22						2.347296355	4.561552812
23						2.311107817	4.481194304
24						2.239123278	4.460504870
25						2.209056926	4.342923082
26						2	4.302775637
27						1.837852791	4.246979603
28						1.789244119	4.143864425
29						1.726109445	4.061498850
30						1.697224362	4
31						1.537401577	3.847759065
32						1.438447187	3.618033988
33						1	3
34						0.807417596	2.858441954
35						0.753020395	2.765366864
36						0.697224362	2.760876721
37						0.661738787	2.688892182
38						0.622797146	2.618033988
39						0.550510257	2.585786437
40						0.544113219	2.554958132
41						0.527166091	2.529316580
42						0.518805695	2.470683419
43						0.438447187	2.428006731
44						0.381966011	2.396338530
45						0.344557618	2.357926367
46						0.300371851	2.334903985
47						0.227777104	2.286462065
48						0.172909084	2.239123278
49						0.120614758	2
50							1.778123837
51							1.763932022
52							1.604068139
53							1.550510257
54							1.381966011
55							1.306177543
56							1.267949192
57							1.234633135
58							1.198062264
59							1
60							0.837722339
61							0.829913513
62							0.801308756
63							0.781690346
64							0.763932022
65							0.728669629
66							0.714857518
67							0.697224362
68							0.657076917
69							0.651105782
70							0.643104132
71							0.627718676
72							0.550510257
73							0.539495129
74							0.485863070
75							0.438447187
76							0.381966011
77							0.354248688
78							0.318669356
79							0.307978528
80							0.300371851
81							0.250882452
82							0.235985074
83							0.216003272
84							0.186393497
85							0.152240934

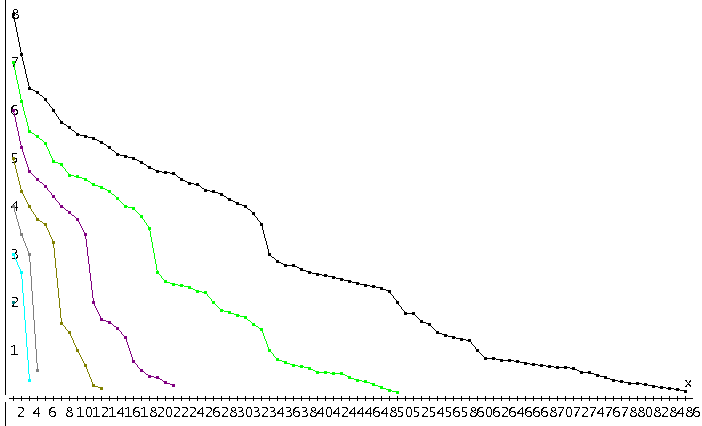
Sorted values of roots for m=1 to 7

Table - number of ways to place m*n nonattacking kings on a 2m x 2n chessboard (for m=1 to 8, n=1 to 20)

n	kings	board	1n/2x2n	kings	board	2n/4x2n	kings	board	3n/6x2n	kings	board	4n/8x2n	kings	board	5n/10x2n	kings	board	6n/12x2n	kings	board	7n/14x2n	kings	board	8n/16x2n
1	1	2x2	4	2	4x2	12	3	6x2	32	4	8x2	80	5	10x2	192	6	12x2	448	7	14x2	1024	8	16x2	2304
2	2	2x4	12	4	4x4	79	6	6x4	408	8	8x4	1847	10	10x4	7698	12	12x4	30319	14	14x4	114606	16	16x4	419933
3	3	2x6	32	6	4x6	408	9	6x6	3600	12	8x6	26040	15	10x6	166368	18	12x6	976640	21	14x6	5392704	24	16x6	28432288
4	4	2x8	80	8	4x8	1847	12	6x8	26040	16	8x8	281571	20	10x8	2580754	24	12x8	21137959	28	14x8	159636030	32	16x8	1134127305
5	5	2x10	192	10	4x10	7698	15	6x10	166368	20	8x10	2580754	25	10x10	32572756	30	12x10	357365350	35	14x10	3544192112	40	16x10	32580145116
6	6	2x12	448	12	4x12	30319	18	6x12	976640	24	8x12	21137959	30	10x12	357365350	36	12x12	5109144543	42	14x12	64737165162	48	16x12	749160010737
7	7	2x14	1024	14	4x14	114606	21	6x14	5392704	28	8x14	159636030	35	10x14	3544192112	42	12x14	64737165162	49	14x14	1027533353168	56	16x14	14677177838054
8	8	2x16	2304	16	4x16	419933	24	6x16	28432288	32	8x16	1134127305	40	10x16	32580145116	48	12x16	749160010737	56	14x16	14677177838054	64	16x16	254977173389319
9	9	2x18	5120	18	4x18	1501674	27	6x18	144605184	36	8x18	7683664202	45	10x18	282359109140	54	12x18	8080813574550	63	14x18	193194265398240	72	16x18
10	10	2x20	11264	20	4x20	5266069	30	6x20	714611200	40	8x20	50123713793	50	10x20	2335042206624	60	12x20	82425144219429	70	14x20	2383116363555182	80	16x20
11	11	2x22	24576	22	4x22	18174084	33	6x22	3449705600	44	8x22	317076250136	55	10x22	18589546217696	66	12x22	803491953235264	77	14x22	27889602664055396	88	16x22
12	12	2x24	53248	24	4x24	61892669	36	6x24	16333065216	48	8x24	1955475353217	60	10x24	143422674213726	72	12x24	7545414941610145	84	14x24	312546900470579954	96	16x24
13	13	2x26	114688	26	4x26	208424880	39	6x26	76081271168	52	8x26	11806000507544	65	10x26	1077891352444220	78	12x26	68680800264413920	91	14x26	3378090945290324892	104	16x26
14	14	2x28	245760	28	4x28	695179339	42	6x28	349524164224	56	8x28	70004699407151	70	10x28	7923134615854816	84	12x28	608889093898882615	98	14x28	35412239480510055916	112	16x28
15	15	2x30	524288	30	4x30	2299608732	45	6x30	1586790140800	60	8x30	408747986045656	75	10x30	57146364209686016	90	12x30	5278006575696293456	105	14x30	361670315347336810428	120	16x30
16	16	2x32	1114112	32	4x32	7552444115	48	6x32	7130144209024	64	8x32	2355077855615435	80	10x32	405497952834408698	96	12x32	44873569636443901967	112	14x32	3611858972942315054336	128	16x32
17	17	2x34	2359296	34	4x34	24648046806	51	6x34	31752978219904	68	8x34	13413115039118042	85	10x34	2836821801400729056	102	12x34	375159494582050088590	119	14x34	35375586671457852212944	136	16x34
18	18	2x36	4980736	36	4x36	79994460139	54	6x36	140298397039232	72	8x36	75623103424916527	90	10x36	19601724610147889574	108	12x36	3090799708762482416287	126	14x36	340648108214969253040772	144	16x36
19	19	2x38	10485760	38	4x38	258339007890	57	6x38	615604372260736	76	8x38	422575531184296006	95	10x38	133975308779739341536	114	12x38	25137927547256761590690	133	14x38	3231742210202924671114360	152	16x38
20	20	2x40	22020096	40	4x40	830619734681	60	6x40	2684534626000512	80	8x40	2342732055500907753	100	10x40	906926114664479185714	120	12x40	202136632706910980639569	140	14x40	30258973227371613303664168	160	16x40

Tabulku hodnot pro šachovnice typu 8 x 2n (pro n=1 až 10) nalezneme už v knize Schach und Zahl (1966), str.53. Je až neuvěřitelné, co dokázal při tehdejší úrovni počítačů Christoph Bandelow vypočítat. Hodnoty ve sloupcích vpravo jsem v tomto případě vygeneroval pomocí vytvořujících funkcí.

A018807 - Number of ways to place n² nonattacking kings on 2n x 2n chessboard
Jinou možností konfigurace králů je případ na obecné čtvercové šachovnici sudých rozměrů 2n x 2n, kam se vejde n² neohrožujících se králů (tedy opět je zaplněna vždy právě čtvrtina šachovnice). V tomto případě je výsledků zatím málo, alespoň odhad průběhu této funkce v článku The Problem of Kings (.ps file) (broken link) - Michael Larsen (The electronic journal of combinatorics 2, 1995). Let f(n) the number of configurations of n² mutually non-attacking kings on a 2n x 2n chessboard
log f(n) = 2n log n - 2n log 2 + O(n^4/5log n)

3.1) Rooks on board n x n - Věže na šachovnici n x n

Na doplnění ještě uvádím vzorce pro počet postavení k neohrožujících se věží na šachovnici n x n. Jako jediný z těchto problémů byl tento zcela vyřešen, obecný vzorec je
k rooks, board nxn: (COMB(n,k))²*k!
kde COMB(n,k)=n!/k!/(n-k)! je kombinační číslo ("n nad k")
Objevit tento vzorec je poměrně snadné, cituje jej třeba už Wilhelm Ahrens Mathematische unterhaltungen und spiele (1901).

Speciálně pokud k=n, vychází počet možných pozic n neohrožujících se věží na šachovnici n x n roven n! (n faktoriál)
n rooks, board nxn: n!
2 rooks, board nxn: n²(n-1)²/2
3 rooks, board nxn: n²(n-1)²(n-2)²/6

Pro srovnání s ostatními vzorci, počet těchto kombinací je také polynom, po roznásobení dostaneme jeho koeficienty ve tvaru:
n!²/(n-k)!²/k! = n^2k/k! +
n^2k-1*(-1)¹/k!/1! *k(k-1) +
n^2k-2*(-1)²/k!/2! *k(k-1)(3k²-5k+1)/3 +
n^2k-3*(-1)³/k!/3! *k²(k-1)³(k-2) +
n^2k-4*(-1)⁴/k!/4! *k(k-1)(k-2)(15k⁵-75k⁴+125k³-81k²+7k+3)/15 +
n^2k-5*(-1)⁵/k!/5! *k²(k-1)²(k-2)(k-3)(3k⁴-14k³+21k²-10k-3)/3 +
n^2k-6*(-1)⁶/k!/6! *k(k-1)(k-2)(k-3)(63k⁸-630k⁷+2457k⁶-4753k⁵+4557k⁴-1453k³-612k²+131k+60)/63 +
n^2k-7*(-1)⁷/k!/7! *k²(k-1)²(k-2)(k-3)(k-4)(9k⁷-90k⁶+348k⁵-646k⁴+530k³-20k²-191k-60)/9 +
n^2k-8*(-1)⁸/k!/8! *k(k-1)(k-2)(k-3)(k-4)(135k¹¹-2250k¹⁰+15615k⁹-58650k⁸+128275k⁷-158510k⁶+84541k⁵+23230k⁴-32495k³-13610k²+4269k+1890)/135 +
n^2k-9*(-1)⁹/k!/9! *k²(k-1)²(k-2)(k-3)(k-4)(k-5)(15k¹⁰-255k⁹+1800k⁸-6806k⁷+14609k⁶-16481k⁵+4880k⁴+7966k³-3349k²-6159k-1890)/15 +
n^2k-10*(-1)¹⁰/k!/10!*k(k-1)(k-2)(k-3)(k-4)(k-5)(99k¹⁴-2475k¹³+26730k¹²-163581k¹¹+622974k¹⁰-1513325k⁹+2253768k⁸-1668051k⁷-200574k⁶+1086969k⁵+144402k⁴-705343k³-261879k²+108126k+45360)/99 +
n^2k-11*(-1)¹¹/k!/11!*k²(k-1)²(k-2)(k-3)(k-4)(k-5)(k-6)(9k¹³-231k¹²+2559k¹¹-15999k¹⁰+61679k⁹-148707k⁸+208749k⁷-112209k⁶-106467k⁵+138243k⁴+110077k³-120297k²-153486k-45360)/9 + ...

Problém byl vyřešen i na obdélníkových šachovnicích, počet pozic k neohrožujících se věží na šachovnici m x n je:
(m! n!) / ((m-k)! (n-k)! k!)

Viz též Rook Polynomial nebo Rook Polynomials (broken link)

3.2) Rooks on board k x n - Věže na šachovnici k x n

Z předchozího vzorce pro obecnou obdélníkovou šachovici vyplývá (při m=k) tento vzorec pro
k rooks, board kxn: n!/(n-k)!

Pro srovnání s ostatními vzorci, počet těchto kombinací je také polynom, po roznásobení dostaneme jeho koeficienty ve tvaru:
n!/(n-k)! = n^k -
n^k-1*k(k-1)/2 +
n^k-2*k(k-1)(k-2)(3k-1)/24 -
n^k-3*k²(k-1)²(k-2)(k-3)/48 +
n^k-4*k(k-1)(k-2)(k-3)(k-4)(15k³-30k²+5k+2)/5760 -
n^k-5*k²(k-1)²(k-2)k-3)(k-4)(k-5)(3k²-7k-2)/11520 +
n^k-6*k(k-1)(k-2)(k-3)(k-4)(k-5)(k-6)(63k⁵-315k⁴+315k³+91k²-42k-16)/2903040 - ...

Obecně má nejvyšší člen každého rozvoje tvar:
n^k-i * k²ⁱ / 2ⁱ / i! + ...

Při použití kombinačních čísel (např. "k nad 12" je k!/(k-12)!/12!) lze zápis tohoto výrazu trochu zjednodušit:
n!/(n-k)! = n^k +
n^k-1 *(-1)¹ *COMB(k,2) /2¹ *2 +
n^k-2 *(-1)² *COMB(k,3) /2² *(3k-1) +
n^k-3 *(-1)³ *COMB(k,4) /2³ *4k(k-1) +
n^k-4 *(-1)⁴ *COMB(k,5) /2⁴ *(15k³-30k²+5k+2)/3 +
n^k-5 *(-1)⁵ *COMB(k,6) /2⁵ *2k(k-1)(3k²-7k-2) +
n^k-6 *(-1)⁶ *COMB(k,7) /2⁶ *(63k⁵-315k⁴+315k³+91k²-42k-16)/9 +
n^k-7 *(-1)⁷ *COMB(k,8) /2⁷ *8k(k-1)(9k⁴-54k³+51k²+58k+16)/9) +
n^k-8 *(-1)⁸ *COMB(k,9) /2⁸ *(135k⁷-1260k⁶+3150k⁵-840k⁴-2345k³-540k²+404k+144)/15 +
n^k-9 *(-1)⁹ *COMB(k,10)/2⁹ *2k(k-1)(15k⁶-165k⁵+465k⁴+17k³-648k²-548k-144)/3 +
n^k-10*(-1)¹⁰*COMB(k,11)/2¹⁰*(99k⁹-1485k⁸+6930k⁷-8778k⁶-8085k⁵+8195k⁴+11792k³+2068k²-2288k-768)/9 +
n^k-11*(-1)¹¹*COMB(k,12)/2¹¹*4k(k-1)(9k⁸-156k⁷+834k⁶-1080k⁵-1927k⁴+1252k³+4156k²+3056k+768)/3 + ...

Koeficienty těchto polynomů se nazývají Stirlingova čísla prvního druhu, viz Stirling Numbers of the First Kind. Jsou sice známy rekurentní vzorce pro tyto koeficienty (viz např. Stirling's polynomials), ale explicitní vzorce byly doposud publikovány jen do úrovně 5, ostatní vzorce (výrazy od k-6 dále) jsou pravděpodobně mým objevem (V. Kotěšovec, 9.2.2010). Viz také OEIS - A112002.

4.1) Bishops on board n x n - Střelci na šachovnici n x n

Vzorce pro počet pozic neohrožujících se střelců na šachovnici n x n najdeme např. v knize Schach und Zahl, 1966 (str.58-62), jejímž autorem je Karl Fabel, který většinu následujících vzorců sám objevil.

2 bishops, board nxn: n(n-1)(3n²-n+2)/6

3 bishops, board nxn: n(n-2)(2n⁴-4n³+7n²-6n+4)/12, pro n sudé (even), (K. Fabel, 1966)
3 bishops, board nxn: (n-1)(2n⁵-6n⁴+9n³-11n²+5n-3)/12, pro n liché (odd), (K. Fabel, 1966)

4 bishops, board nxn: n(n-2)(15n⁶-90n⁵+260n⁴-524n³+727n²-646n+348)/360, pro n sudé (even), (K. Fabel, 1966)
4 bishops, board nxn: (n-1)(n-2)(15n⁶-75n⁵+185n⁴-339n³+388n²-258n+180)/360, pro n liché (odd), (K. Fabel, 1966 - tento vzorec sice není v knize "Schach und Zahl" uveden, ale předpokládám, že ho také objevil - nyní jsem ho vygeneroval a potvrdil počítačem)

5 bishops, board nxn: n(n-2)(3n⁸-34n⁷+177n⁶-590n⁵+1435n⁴-2592n³+3326n²-2844n+1344)/360, pro n sudé (even), (V. Kotesovec, 26.1.2010)
5 bishops, board nxn: (n-1)(n-2)(n-3)(3n⁷-22n⁶+80n⁵-204n⁴+379n³-464n²+378n-270)/360, pro n liché (odd), (V. Kotesovec, 26.1.2010)

Obecný vzorec není znám, ale první členy polynomu mají vždy tvar n^2k/k! - 2n^2k-1/3/(k-2)! + ...
Zatímco v případě dam a věží byl vždy počet kamenů maximálně n (k≤n), v případě střelců (i jezdců) může být takový počet větší než n. Horní omezení pro maximální počet střelců je 2n-2, více viz Bishops Problem.

Linky na OEIS
A172123 - 2 bishops NxN
A172124 - 3 bishops NxN
A172127 - 4 bishops NxN
A172129 - 5 bishops NxN

Nevím kdo je autorem vzorce pro k=2, ale (kromě Fabela) jej cituje již Henry Dudeney ve své knize "Amusements in Mathematics" (1917), str.96.

n	2 bishops	3 bishops	4 bishops	5 bishops
2	4	0	0
3	26	26	8	0
4	92	232	260	112
5	240	1124	2728	3368
6	520	3896	16428	39680
7	994	10894	70792	282248
8	1736	26192	242856	1444928
9	2832	56296	706048	5865552
10	4380	110960	1809464	20014112
11	6490	204130	4199064	59673360
12	9284	355000	8992684	159698416
13	12896	589196	18024072	391202680
14	17472	940072	34170724	890095584
15	23170	1450134	61784632	1902427800
16	30160	2172576	107243472	3853570560
17	38624	3172944	179645376	7450556064
18	48756	4530912	291667440	13829016768
19	60762	6342186	460615272	24759442464
20	74860	8720520	709686228	42930138864
21	91280	11799860	1069477928	72328779720
22	110264	15736600	1579767068	118747638592
23	132066	20711966	2291594536	190443610280

4.2) Bishops on board k x n - Střelci na šachovnici k x n

2 bishops, board 2xn: 2n²-3n+2
3 bishops, board 3xn: (9n³-45n²+106n-108)/2, n>=4, (V. Kotesovec, 26.1.2010)
4 bishops, board 4xn: (32n⁴-336n³+1702n²-4701n+5844)/3, n>=9, (V. Kotesovec, 26.1.2010)
5 bishops, board 5xn: (625n⁵-11250n⁴+98875n³-515250n²+1566016n-2194944)/24, n>=16, (V. Kotesovec, 26.1.2010)
6 bishops, board 6xn: (648n⁶-17820n⁵+240930n⁴-2011545n³+10806047n²-35094560n+53430940)/10, n>=25, (V. Kotesovec, 28.1.2010)

První členy těchto vzorců mají obecně tvar (kn)^k/k! - (kn)^k-1(2k-1)/2/(k-2)! + ...
Jiný možný zápis je (kn)^k/k! - (kn)^k-1*comb(2k-1,2)/2/(k-1)! + ...
kde comb(2k-1,2) je kombinační číslo "2k-1 nad 2".

OEIS linky:
A172207 - 3 bishops 3 X n
A172208 - 4 bishops 4 X n
A172210 - 5 bishops 5 X n
A172211 - 6 bishops 6 X n

n	2 bishops	3 bishops	4 bishops	5 bishops	6 bishops
2	4	6	9	12	16
3	11	26	61	143	313
4	22	86	260	770	2320
5	37	211	927	3368	12160
6	56	426	2578	12632	53744
7	79	758	5965	38566	209428
8	106	1234	12066	98968	683524
9	137	1881	22135	222351	1905625
10	172	2726	37678	450682	4664384
11	211	3796	60457	843169	10297579
12	254	5118	92488	1479116	20907590
13	301	6719	136043	2460912	39664250
14	352	8626	193650	3917228	71114916
15	407	10866	268093	6006056	121559433
16	466	13466	362412	8917888	199459466
17	529	16453	479903	12878847	315906248
18	596	19854	624118	18153806	485124352
19	667	23696	798865	25049515	725031335
20	742	28006	1008208	33917724	1057839684
21	821	32811	1256467	45158308	1510706686
22	904	38138	1548218	59222392	2116429956
23	991	44014	1888293	76615476	2914190277
24	1082	50466	2281780	97900560	3950340692
25	1177	57521	2734023	123701269	5279242444
26	1276	65206	3250622	154704978	6964147544
27	1379	73548	3837433	191665937	9078128011
28	1486	82574	4500568	235408396	11705051758
29	1597	92311	5246395	286829730	14940605138
30	1712	102786	6081538	346903564	18893362144
31	1831	114026	7012877	416682898	23685900265
32	1954	126058	8047548	497303232	29455962998

5.1) Knights on board n x n - Jezdci na šachovnici n x n

Vzorce pro počet pozic neohrožujících se jezdců na šachovnici n x n.
2 knights, board nxn: (n-1)(n+4)(n²-3n+4)/2, (E.Lucas, 1891)

3 knights, board nxn: (n-2)(n+5)(n⁴-3n³-8n²+66n-108)/6, n>=4 , (K. Fabel, 1966)

4 knights, board nxn: (n⁸-54n⁶+144n⁵+1019n⁴-5232n³-2022n²+51120n-77184)/24, n>=6 (K. Fabel, 1966)

5 knights, board nxn: (n¹⁰-90n⁸+240n⁷+3235n⁶-16320n⁵-40530n⁴+396480n³-231656n²-3359520n+6509280)/120, n>=8 (V. Kotesovec, 25.1.2010)

Obecný vzorec není znám, ale první členy polynomu mají vždy tvar n^2k/k! - 9n^2k-2/2/(k-2)! + 12n^2k-3/(k-2)! +...
Také v případě jezdců může být jejich počet větší než n (pro šachovnici 8x8 dokonce 32), obecně je tento maximální počet n²/2 (pro n>2 sudé) a (n²+1)/2 (pro n>1 liché), více viz Knights Problem

Linky na OEIS
A172132 - 2 knights NxN
A172134 - 3 knights NxN
A172135 - 4 knights NxN
A172136 - 5 knights NxN

Viz Edouard Lucas: Théorie des nombres (1891), vzorec pro počet rozmístění 2 neohrožujících se jezdců najdeme na str.98 (zde jsou správně znaménka, ale vypadl znak "p"), viz též Edouard Lucas: Récréations mathématiques (1894), str.132 (ve vzorci je však tisková chyba, před členem p² má být +, ne -. Správně má být tedy (p-1)(p³+p²-8p+16)/2)

n	2 knights	3 knights	4 knights	5 knights
2	6	4	1
3	28	36	18	2
4	96	276	412	340
5	252	1360	4436	9386
6	550	4752	26133	97580
7	1056	13340	111066	649476
8	1848	32084	376560	3184708
9	3016	68796	1080942	12472084
10	4662	135040	2732909	41199404
11	6900	247152	6253408	119171110
12	9856	427380	13204356	309957412
13	13668	705144	26100160	739123094
14	18486	1118416	48819677	1639655452
15	24472	1715220	87137934	3422020324
16	31800	2555252	149398608	6778432292
17	40656	3711620	247349946	12833460256
18	51238	5272704	397168485	23356032940
19	63756	7344136	620696612	41051290730
20	78432	10050900	946921684	69954580804

5.2) Knights on board k x n - Jezdci na šachovnici k x n

2 knights, board 2xn: 2n²-3n+4, n>=2
3 knights, board 3xn: (9n³-45n²+122n-144)/2, n>=4, (V. Kotesovec, 26.1.2010)
4 knights, board 4xn: 8(4n⁴-36n³+170n²-450n+537)/3, n>=6, (V. Kotesovec, 26.1.2010)
5 knights, board 5xn: (625n⁵-8250n⁴+57235n³-242778n²+608440n-705984)/24, n>=8, (V. Kotesovec, 26.1.2010)
6 knights, board 6xn: (648n⁶-11340n⁵+103770n⁴-606645n³+2328317n²-5466660n+6051720)/10, n>=10, (V. Kotesovec, 26.1.2010)
7 knights, board 7xn: (117649n⁷-2571471n⁶+29223943n⁵-216954465n⁴+1114503256n³-3907492824n²+8562799512n-8962924320)/720, n>=12, (V. Kotesovec, 29.1.2010)
8 knights, board 8xn: (262144n⁸-6881280n⁷+93456384n⁶-838693632n⁵+5361604836n⁴-24739168020n³+79766188151n²-163079018193n+160750559340)/630, n>=14, (V. Kotesovec, 27.3.2010)

První členy těchto vzorců mají obecně tvar (kn)^k/k! - 3(k-1)(3k-4)(kn)^k-1/k!/2 + ...
Jiný možný zápis je (kn)^k/k! - comb(3k-3,2)*(kn)^k-1/k! + ...
kde comb(3k-3,2) je kombinační číslo "3k-3 nad 2".

OEIS linky:
A172212 - 3 knights 3 X n
A172213 - 4 knights 4 X n
A172214 - 5 knights 5 X n
A172215 - 6 knights 6 X n
A172217 - 7 knights 7 X n
A174698 - 8 knights 8 X n

n	2 knights	3 knights	4 knights	5 knights	6 knights	7 knights	8 knights
2	6	12	16	28	58	78	81
3	13	36	84	259	729	1758	4409
4	24	100	412	1968	8830	38588	175720
5	39	233	1416	9386	60285	383246	2479881
6	58	456	3640	30842	257318	2135344	17925691
7	81	796	7928	82738	858262	8891854	92952858
8	108	1280	15384	192336	2404448	30108310	379978716
9	139	1935	27352	400277	5879329	86669806	1286959255
10	174	2788	45432	763984	12927182	219845764	3765248749
11	213	3866	71480	1360797	26115008	504261973	9805497200
12	256	5196	107608	2291056	49238436	1065642840	23226916560
13	303	6805	156184	3681226	87675623	2104251027	50866495373
14	354	8720	219832	5687022	148787822	3924818982	104288896551
15	409	10968	301432	8496534	242366502	6973786593	202154535834
16	468	13576	404120	12333352	381127124	11884673662	373400685738
17	531	16571	531288	17459691	581249573	19532410762	661407061211
18	598	19980	686584	24179516	862965246	31097451768	1129334088897
19	669	23830	873912	32841667	1251190796	48140491605	1866838857216
20	744	28148	1097432	43842984	1776208532	72688612756	2998390521676
21	823	32961	1361560	57631432	2474393475	107333684073	4693423716457
22	906	38296	1670968	74709226	3388987070	155343835434	7178585300523
23	993	44180	2030584	95635956	4570917554	220788831789	10752346543734
24	1084	50640	2445592	121031712	6079666980	308680170138	15802269635646
25	1179	57703	2921432	151580209	7984184897	425126722984	22825234176903

5.3) Knights on cylindrical board n x n - Jezdci na válcové šachovnici n x n

Válcová šachovnice (vertical cylinder, Vertikalzylinder) je šachovnice stočená do válce tak, aby okrajové sloupce byly vedle sebe. Vertical cylinder - board with a- and h- files alongside one another.

2 knights, board nxn: n(n³-9n+12)/2, n>=5, (V. Kotesovec, 31.1.2010)
3 knights, board nxn: n(n-3)(n⁴+3n³-18n²-18n+164)/6, n>=6, (V. Kotesovec, 31.1.2010)
4 knights, board nxn: n(n⁷-54n⁵+72n⁴+1115n³-2616n²-8502n+26712)/24, n>=9, (V. Kotesovec, 31.1.2010)
5 knights, board nxn: n(n⁹-90n⁷+120n⁶+3395n⁵-8160n⁴-62130n³+204000n²+463464n-1888080)/120, n>=10, (V. Kotesovec, 31.1.2010)

První členy polynomu mají vždy tvar n^2k/k! - 9n^2k-2/2/(k-2)! + 6n^2k-3/(k-2)! + ...

Počet pozic na válcové šachovnici n x n je vždy dělitelný n (to odpovídá tomu, že každou pozici je možno libovolně posunout doleva nebo doprava aniž by se nějak změnilo vzájemné napadání kamenů.)

OEIS linky:
A172964 - 2 knights cylindrical NxN
A172965 - 3 knights cylindrical NxN
A172966 - 4 knights cylindrical NxN
A172967 - 5 knights cylindrical NxN

n	2 knights	3 knights	4 knights	5 knights
2	4	0	0
3	18	6	0	0
4	92	240	306	208
5	230	1010	2365	3210
6	522	4056	19047	58056
7	1022	12068	90503	458157
8	1808	30000	328324	2524176
9	2970	65628	981693	10587591
10	4610	130480	2547955	36576380
11	6842	240856	5933257	109008735
12	9792	418968	12681288	289450344
13	13598	694200	25284363	700477401
14	18410	1104488	47595023	1570789892
15	24390	1697820	85357395	3304892985
16	31712	2533856	146879312	6586928032
17	40562	3685668	243867873	12530769343
18	51138	5241600	392452803	22891446252

5.4) Knights on toroidal board n x n - Jezdci na prstencové šachovnici n x n

Prstencová šachovnice je kombinace vertikální a horizontální válcové šachovnice. Toroidal chessboard (anchor-ring) - board on which the a- and h-files are joined and the bottom and top ranks are also joined. The anchor-ring is a combination of the vertical and horizontal cylinders.

2 knights, board nxn: n²(n+3)(n-3)/2, n>=5, (V. Kotesovec, 31.1.2010)
3 knights, board nxn: n²(n⁴-27n²+218)/6, n>=6, (V. Kotesovec, 31.1.2010)
4 knights, board nxn: n²(n⁶-54n⁴+1115n²-8934)/24, n>=9, (V. Kotesovec, 31.1.2010)
5 knights, board nxn: n²(n⁸-90n⁶+3395n⁴-64290n²+522504)/120, n>=10, (V. Kotesovec, 31.1.2010)
6 knights, board nxn: n²(n¹⁰-135n⁸+8005n⁶-262665n⁴+4816354n²-39858840)/720, n>=13, (V. Kotesovec, 31.1.2010)
7 knights, board nxn: n²(n¹²-189n¹⁰+16135n⁸-801255n⁶+24595984n⁴-445931556n²+3756080880)/5040, n>=14, (V. Kotesovec, 18.2.2010)

První členy polynomu mají vždy tvar n^2k/k! - 9n^2k-2/2/(k-2)! + (243k+143)*n^2k-4/24/(k-3)! - ...

Počet pozic na prstencové šachovnici n x n je vždy dělitelný n² (to odpovídá tomu, že každou pozici je možno libovolně posunout ve směru obou os x nebo y aniž by se nějak změnilo vzájemné napadání kamenů). V případě bodových kamenů se se zvětšujícím se n zmenšuje rozdíl mezi normální a prstencovou šachovnicí, naopak v případě liniových kamenů tento rozdíl zůstává.

OEIS linky:
A172529 - 2 knights toroidal NxN
A172530 - 3 knights toroidal NxN
A172531 - 4 knights toroidal NxN
A172532 - 5 knights toroidal NxN
A172533 - 6 knights toroidal NxN
A173436 - 7 knights toroidal NxN

n	2 knights	3 knights	4 knights	5 knights	6 knights	7 knights
2	2	0	0
3	18	6	0	0	0	0
4	88	208	228	128	56	16
5	200	600	600	120	0	0
6	486	3252	12357	30312	54972	80352
7	980	10584	68796	283906	764596	1359288
8	1760	27584	275888	1872064	8972896	31404480
9	2916	61992	872532	8643186	62560728	339256836
10	4550	125300	2344025	31702920	322246800	2527519400
11	6776	233772	5580762	98179400	1323868260	14053530964
12	9720	409584	12107196	267487920	4595943336	63100177488
13	13520	682084	24392446	659015500	14000143196	240356217660
14	18326	1089172	46261537	1496908840	38413461800	803630856504
15	24300	1678800	83426400	3179369070	96746410800	2416671974700
16	31616	2510592	144157632	6382030592	226834407552	6655251717376
17	40460	3657584	240119696	12207535134	500492572112	17015566051020
18	51030	5208084	387393921	22396355496	1048044384360	40822003107000
19	63536	7267652	607715342	39617305308	2096986629308	92679987456312
20	78200	9961200	929951100	67860021680	4031211268200	200490192134800

6.1) Nightriders on board n x n - Tátoši na šachovnici n x n

Vzorce pro počet pozic neohrožujících se tátošů na šachovnici n x n. Tátoš je liniový kámen s jednotkovým tahem jezdce. Nightrider is rider [1,2].

2 nightriders, board nxn: n(3n³-5n²+9n-4)/6, pro n sudé (even), (C. Poisson, Rex Multiplex 29/1990, p.829)
2 nightriders, board nxn: n(n-1)(3n²-2n+7)/6, pro n liché (odd), (C. Poisson, Rex Multiplex 29/1990, p.829)

3 nightriders, board nxn:
1/6*n⁶-5/6*n⁵+4031/1440*n⁴-621/100*n³+3313/288*n²-2623/150*n+82321/43200
+ (1/4*n³-25/32*n²+77/50*n-43/64)*(-1)ⁿ
- (1+(-1)ⁿ)/8*cos(pi*n/2)
+ 8/27*(-1)ⁿ*cos(pi*n/3)
+ (-4*(-1)ⁿ+(sqrt(5)+3+(1-sqrt(5)/5)*(-1)ⁿ)*n)*4/25*cos(pi*n/5)
+ (sqrt(58*sqrt(5)+130)-sqrt(50-22*sqrt(5))*(-1)ⁿ/5)*16/25*sin(pi*n/5)
+ (-4+(sqrt(5)/5+1+(3-sqrt(5))*(-1)ⁿ)*n)*4/25*cos(2*pi*n/5)
+ (sqrt(22*sqrt(5)+50)/5-sqrt(130-58*sqrt(5))*(-1)ⁿ)*16/25*sin(2*pi*n/5), (V. Kotesovec, 18.2.2010)

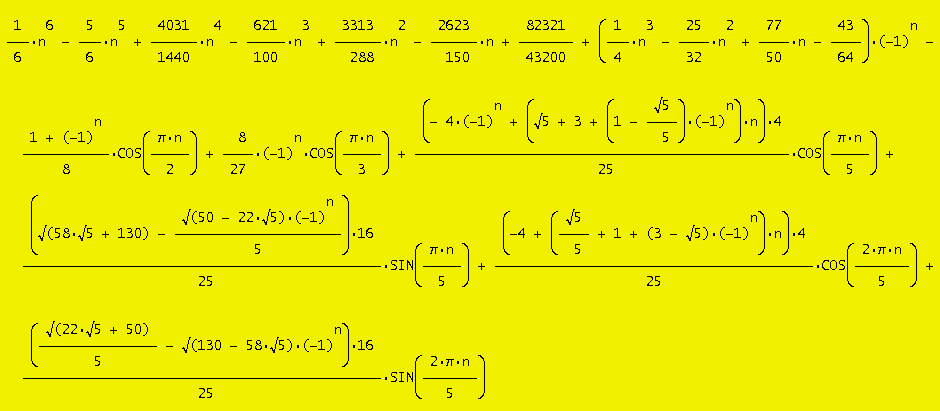
exact formula by Vaclav Kotesovec

Rekurentní vzorec:
a_n = 2a_n-1-a_n-3-2a_n-5+2a_n-6+a_n-8-3a_n-11+2a_n-13+4a_n-15-4a_n-16-2a_n-18+3a_n-20-a_n-23-2a_n-25+2a_n-26+a_n-28-2a_n-30+a_n-31, n>=32

Výše uvedený vzorec lze zapsat také ve formě tabulky takto:
n⁶/6-5*n⁵/6+4031*n⁴/1440-621/100*n³+3313/288*n² -C_n*n+D_n + (1/4*n³-25/32*n²)*(-1)ⁿ

Konstanty C_n a D_n se opakují s periodou 60, tedy podle zbytku n při dělení 60, kde n je rozměr šachovnice n x n. Existuje tak 60 různých vzorců podle toho, zda je n tvaru 60a, 60a+1, ... , 60a+59 (kde a je celé nezáporné číslo). Konstanta C_n má kratší periodu 10.

n MOD 60	C_n	D_n	C_n, D_n periods
0	44/3	0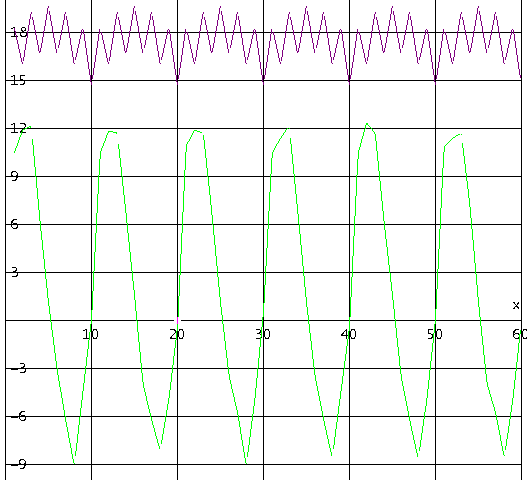
1	1379/75	75091/7200
2	1196/75	5353/450
3	1451/75	9723/800
4	1244/75	1412/225
5	59/3	331/288
6	1244/75	-151/50
7	1451/75	-44717/7200
8	1196/75	-2044/225
9	1379/75	-3589/800
10	44/3	1/18
11	1379/75	75091/7200
12	1196/75	296/25
13	1451/75	84307/7200
14	1244/75	3049/450
15	59/3	51/32
16	1244/75	-892/225
17	1451/75	-44717/7200
18	1196/75	-407/50
19	1379/75	-35501/7200
20	44/3	-4/9
21	1379/75	8699/800
22	1196/75	5353/450
23	1451/75	84307/7200
24	1244/75	168/25
25	59/3	331/288
26	1244/75	-1559/450
27	1451/75	-4613/800
28	1196/75	-2044/225
29	1379/75	-35501/7200
30	44/3	1/2
31	1379/75	75091/7200
32	1196/75	2564/225
33	1451/75	9723/800
34	1244/75	3049/450
35	59/3	331/288
36	1244/75	-88/25
37	1451/75	-44717/7200
38	1196/75	-3863/450
39	1379/75	-3589/800
40	44/3	-4/9
41	1379/75	75091/7200
42	1196/75	617/50
43	1451/75	84307/7200
44	1244/75	1412/225
45	59/3	51/32
46	1244/75	-1559/450
47	1451/75	-44717/7200
48	1196/75	-216/25
49	1379/75	-35501/7200
50	44/3	1/18
51	1379/75	8699/800
52	1196/75	2564/225
53	1451/75	84307/7200
54	1244/75	361/50
55	59/3	331/288
56	1244/75	-892/225
57	1451/75	-4613/800
58	1196/75	-3863/450
59	1379/75	-35501/7200

Z výše uvedeného obecného vzorce vyplývají vzorce pro:
C_n = 2623/150 - 77/50*(-1)ⁿ - (sqrt(5)+3+(1-sqrt(5)/5)*(-1)ⁿ)*4/25*cos(pi*n/5) - (sqrt(5)/5+1+(3-sqrt(5))*(-1)ⁿ)*4/25*cos(2*pi*n/5)

D_n = 82321/43200-1/8*cos(pi*n/2)-16/25*cos(2*pi*n/5)+16/25*sqrt(58*sqrt(5)+130)*sin(pi*n/5)+16/125*sqrt(22*sqrt(5)+50)*sin(2*pi*n/5)
+ (-1)ⁿ*(-43/64-1/8*cos(pi*n/2)+8/27*cos(pi*n/3)-16/25*cos(pi*n/5)-sqrt(50-22*sqrt(5))*16/125*sin(pi*n/5)-sqrt(130-58*sqrt(5))*16/25*sin(2*pi*n/5))

Obecný vzorec byl ověřen na prvních 310 hodnotách.

Linky v OEIS
A172141 - 2 nightriders NxN
A173429 - 3 nightriders NxN

n	2 nightriders	3 nightriders	4 nightriders
2	6	4	1
3	28	36	18
4	96	276	412
5	240	1152	3046
6	518	3920	17365
7	980	10568	68540
8	1712	25348	232164
9	2784	53848	655852
10	4310	106292	1680033
11	6380	194732	3855946
12	9136	339416	8279704
13	12688	562652	16532026
14	17206	899796	31456369
15	22820	1388008	56832396
16	29728	2083908	99009508
17	38080	3044992	165941072
18	48102	4356344	270328605
19	59964	6102144	427383994
20	73920	8404204	660479212
21	90160	11380564	996624154
22	108966	15199100	1476091049
23	130548	20019856	2144134416
24	155216	26067112	3066551576
25	183200	33551812	4315580852
26	214838	42766092	5994143473
27	250380	53981600	8213049038
28	290192	67570804	11127498228
29	334544	83876732	14901856642
30	383830	103365728	19763006661
31	438340	126463668	25947796192
32	498496	153745412	33779182556
33	564608	185732188	43590211584
34	637126	223122948	55829979313
35	716380	266547472	70956669486
36	802848	316845560	89582262248
37	896880	374769664	112325177234
38	998982	441318188	140004466369
39	1109524	517381252	173440817244
40	1229040	604134684	213712999188
41	1357920	702622052	?
42	1496726	814216544	?
43	1645868	940132020	?
44	1805936	1081959860	?
45	1977360	1241101728	?
46	2160758	1419389236	?
47	2356580	1618430292	?
48	2565472	1840319784	?
49	2787904	2086891176	?
50	3024550	2360526732	?
51	3275900	2663305556	?
52	3542656	2997922516	?
53	3825328	3366723560	?
54	4124646	3772742240	?
55	4441140	4218613152	?
56	4775568	4707735876	?
57	5128480	5243056424	?
58	5500662	5828368716	?
59	5892684	6466953812	?
60	6305360	7163029360	?
61	6739280	7920235852	?
62	7195286	8743245188	?
63	7673988	9636082848	?
64	8176256	10603906308	?
65	8702720	11651152152	?
66	9254278	12783496072	?
67	9831580	14005812832	?
68	10435552	15324329940	?
69	11066864	16744388300	?
70	11726470	18272801892	?
71	12415060	19915406448	?
72	13133616	21679638248	?
73	13882848	23571857756	?
74	14663766	25600160124	?
75	15477100	27771460968	?
76	16323888	30094552244	?
77	17204880	32576936124	?
78	18121142	35228140248	?
79	19073444	38056285612	?
80	20062880	41071675484	?
81	21090240	44283082684	?
82	22156646	47701627220	?
83	23262908	51336767992	?
84	24410176	55200483576	?
85	25599280	59302953672	?
86	26831398	63657058652	?
87	28107380	68273734740	?
88	29428432	73166808260	?
89	30795424	78348008556	?
90	32209590	83832153128	?
91	33671820	89631801732	?
92	35183376	95762809460	?
93	36745168	102238605096	?
94	38358486	109076128388	?
95	40024260	116289716172	?
96	41743808	123897441384	?
97	43518080	131914588952	?
98	45348422	140360414436	?
99	47235804	149251191772	?
100	49181600	158607409644	?

6.2) Nightriders on board k x n - Tátoši na šachovnici k x n

2 nightriders, board 2xn: 2n²-3n+4, n>=2
3 nightriders, board 3xn: (9n³-57n²+210n-344)/2, n>=8, (V. Kotesovec, 26.1.2010)
4 nightriders, board 4xn: (32n⁴-432n³+3190n²-13323n+25530)/3, n>=18, (V. Kotesovec, 26.1.2010)
5 nightriders, board 5xn: (625n⁵-15250n⁴+197915n³-1588634n²+7645896n-17283552)/24, n>=32, (V. Kotesovec, 28.1.2010)

OEIS linky:
A172218 - 3 nightriders 3 X n
A172219 - 4 nightriders 4 X n
A172220 - 5 nightriders 5 X n

n	2 nightriders	3 nightriders	4 nightriders	5 nightriders	6 nightriders
2	6	12	16	28	58
3	13	36	84	157	315
4	24	100	412	1248	3862
5	39	213	1126	4650	19419
6	58	408	2760	15162	85358
7	81	712	5739	37988	256549
8	108	1148	10982	86958	706060
9	139	1745	19695	181423	1689706
10	174	2528	33068	351708	3745158
11	213	3524	52801	648441	7737606
12	256	4760	80638	1127392	15042498
13	303	6263	118731	1874194	28033286
14	354	8060	169368	2988466	49685456
15	409	10178	235135	4602096	84688103
16	468	12644	318890	6870240	138994668
17	531	15485	423733	9983347	220999518
18	598	18728	553028	14163972	341148264
19	669	22400	710389	19672403	513146177
20	744	26528	899690	26812260	753927570
21	823	31139	1125059	35929480	1084629369
22	906	36260	1390880	47418482	1530923606
23	993	41918	1701793	61723238	2123729778
24	1084	48140	2062694	79341720	2900209972
25	1179	54953	2478735	100828175	3904141919
26	1278	62384	2955324	126796852	?
27	1381	70460	3498125	157924785	?
28	1488	79208	4113058	194954956	?
29	1599	88655	4806299	238699512	?
30	1714	98828	5584280	290042826	?
31	1833	109754	6453689	349944662	?
32	1956	121460	7421470	419443276	?
33	2083	133973	8494823	499658555	?
34	2214	147320	9681204	591795132	?
35	2349	161528	10988325	697145517	?
36	2488	176624	12424154	817093220	?
37	2631	192635	13996915	953115876	?
38	2778	209588	15715088	1106788370	?
39	2929	227510	17587409	1279785962	?
40	3084	246428	19622870	1473887412	?

7.1) Amazons (superqueens) on board n x n - Amazonky na šachovnici n x n

Amazonka je kombinovaný kámen s pohyblivostí dámy a jezdce. Amazon (=Superqueen) is queen + knight.

2 amazons, board nxn: (n-1)(n-2)(n-3)(3n+8)/6, (Christian Poisson, 1990)

3 amazons, board nxn: (2n⁶-20n⁵+31n⁴+314n³-1452n²+2040n-672)/12, pro sudá n (even), n>=4, (Panos Louridas, 2007)
3 amazons, board nxn: (2n⁶-20n⁵+31n⁴+314n³-1452n²+2034n-669)/12, pro lichá n (odd), n>=5, (Panos Louridas, 2007)

4 amazons, board nxn: n⁸/24-5n⁷/6+47n⁶/9+43n⁵/10-5053n⁴/24+112585n³/108-15433n²/8+55669n/270+119917/54 + (n³/4-21n²/8+7n-3/2)*(-1)ⁿ + 32/27*(n-1)*COS(2*pi*n/3) + 40*sqrt(3)*SIN(2*pi*n/3)/81, n>=6, (Vaclav Kotesovec, 12.2.2010)

Rekurentní vzorec: a_n = 3a_n-1+a_n-2-9a_n-3+12a_n-5+7a_n-6-15a_n-7-16a_n-8+16a_n-9+15a_n-10-7a_n-11-12a_n-12+9a_n-14-a_n-15-3a_n-16+a_n-17, n>=23

Explicitní vzorec pro 4 amazonky je velmi podobný vzorci pro 4 dámy, periodické členy se SIN a COS jsou shodné a polynom u (-1)ⁿ se liší jen v posledním členu. Rekurentní vzorec je dokonce zcela identický jako pro 4 dámy (sekvence vychází jen z jiných počátečních hodnot).

I když máme zatím příliš málo hodnot, je pravděpodobný průběh této funkce pro k amazonek na šachovnici n x n podobný jako pro dámy:
n^2k/k! - 5/3*n^2k-1/(k-2)! + ...

OEIS linky:
A172200 - 2 amazons (superqueens) n X n
A172201 - 3 amazons (superqueens) n X n
A173214 - 4 amazons (superqueens) n X n

Odkazy:
Christian Poisson, Rex Multiplex 29/1990, str. 829 (v té době vycházející francouzský časopis)
Panos Louridas, idee & form 93/2007, str. 2936-2938 (švýcarský časopis věnovaný skladebnímu šachu)

n	2 amazons	3 amazons	4 amazons
2	0	0	0
3	0	0	0
4	20	0	0
5	92	48	2
6	260	424	112
7	580	1976	1754
8	1120	6616	13074
9	1960	17852	63400
10	3192	41544	234014
11	4920	86660	712248
12	7260	166288	1882132
13	10340	298616	4457246
14	14300	508200	9679760
15	19292	827168	19584514
16	25480	1296744	37367934
17	33040	1968676	67849336
18	42160	2907016	118085614
19	53040	4189772	198107620
20	65892	5910944	321870956
21	80940	8182400	508359070
22	98420	11136168	782972820
23	118580	14926536	1179105738
24	141680	19732600	1740089734
25	167992	25760588	2521359260
26	197800	33246664	3593085246
27	231400	42459476	5043058972
28	269100	53703216	6980158088
29	311220	67320392	9538095102
30	358092	83695144	12879874324
31	410060	103256240	17202560582
32	467480	126480648	22742900942
33	530720	153896756	29783283628
34	600160	186088200	38658709554
35	676192	223697308	49764125812
36	759220	267429184	63562947328
37	849660	318055376	80595959410
38	947940	376418216	101491605140
39	1054500	443434712	126976666126
40	1169792	520101144	157888541850

Problémem n neohrožujících se amazonek na šachovnici n x n se jako první zabýval matematik s přezdívkou Durango Bill, na jeho stránce Durango Bill's - The N-Queens Problem najdeme doposud známé výsledky. Na první pohled se zdá že takové rozestavení pro Amazonky (označované zde jako Superqueen) není možné, ale od šachovnice 10x10 taková řešení existují! Solution exist also for Amazone, N≥10 !
Zkusil jsem vypočítat konstanty pro amazonky podle prvních dvou hypotéz (recomputing constants by both conjectures)
Pro posouzení konvergence obou řad je však zatím k dispozici málo hodnot...

                                                         Durango Bill            Birger Nielsen  Rivin+Vardi+Zimmermann
      Order    < --- Ordinary Queens   --- >             < - Superqueens - >     (f(n)/n!)^(1/(n-1))
      ("N")   Total Solutions   Unique Solutions         Tot. Sol. Unique Sol.                  log(f(n))/(n*log(n))
      --------------------------------------------------------------------------
      1                     1                  1                1              1  
      2                     0                  0                0              0
      3                     0                  0                0              0
      4                     2                  1                0              0
      5                    10                  2                0              0
      6                     4                  1                0              0
      7                    40                  6                0              0
      8                    92                 12                0              0
      9                   352                 46                0              0
      10                  724                 92                4              1  0.2177875229 0.0602059991
      11                 2680                341               44              6  0.2536469800 0.1434663320
      12                14200               1787              156             22  0.2571896108 0.1693509629
      13                73712               9233             1876            239  0.2861405294 0.2260322668
      14               365596              45752             5180            653  0.2780659430 0.2314830981
      15              2279184             285053            32516           4089  0.2863046443 0.2557679703
      16             14772512            1846955           202900          25411  0.2922654623 0.2754751459
      17             95815104           11977939          1330622         166463  0.2973799174 0.2927699845
      18            666090624           83263591          8924976        1115871  0.3013522738 0.3076183338
      19           4968057848          621012754         64492432        8062150  0.3052738993 0.3214276591
      20          39029188884         4878666808        495864256       61984976  0.3090010139 0.3341722647
      21         314666222712        39333324973       3977841852      497236090  0.3122951071 0.3457263661
      22        2691008701644       336376244042      34092182276     4261538564  0.3156003918 0.3566365819
      23       24233937684440      3029242658210     306819842212    38352532487  0.3186994535 0.3667617725
      24      227514171973736     28439272956934    2883202816808   360400504834  0.3215646055 0.3761463830
      25     2207893435808352    275986683743434   28144109776812  3518014210402  0.3241760378 0.3848344687
      26    22317699616364044   2789712466510289                ?              ?             ?            ?

Hodnoty pro N=24 a N=25 vypočítal Wolfram Schubert (2009), (updated 22.1.2010)
Hodnoty pro N=21 až 23 (updated 27.3.2007) jsou převzaty ze stránky "The Oprisch Family Web Site" N x N SuperQueens Solutions Table.

7.2) Amazons (superqueens) on board k x n - Amazonky na šachovnici k x n

Na stránce The Oprisch Family Web Site nalezneme také hodnoty i pro šachovnice k x n, včetně vzorců pro k = 2,3,4,5,6,7 a tabulek hodnot.
2xn:   (n-3)(n-2), n > 3
3xn:   (n-6)(n-5)(n-4), n > 6
4xn:   [(n-7)(n-6)(n-5)(n-4)+(n-10)(n-9)(n-8)(n-7)]/2, n > 7
5xn:   n⁵ -44n⁴ +823n³ -8168n² +42796n -93984, n > 11
6xn:   n⁶ -63n⁵ +1775n⁴ -28613n³ +277462n² -1526716n +3699966, n > 16
7xn:   n⁷ -85n⁶ +3329n⁵ -77911n⁴ +1175240n³ -11392990n² +65448630n -171006180, n > 23

Obecně má polynom tvar: n^k - (k+3)(3k-4)n^k-1/2 + ...

Stejné hodnoty nalezneme také zde: OEIS - A051223, A051224

8.1) Zebras on board n x n - Zebry na šachovnici n x n

Vzorce pro počet pozic neohrožujících se zeber (skokanů [2,3]) na šachovnici n x n. Zebra is leaper [2,3].

2 zebras, board nxn: (n⁴-9n²+40n-48)/2, n>=2, (C. Poisson, Rex Multiplex 29/1990, p.829)

3 zebras, board nxn: (n⁶-27n⁴+120n³+74n²-1608n+2976)/6, n>=6, (V. Kotesovec, 24.1.2010)

4 zebras, board nxn: (n⁸-54n⁶+240n⁵+827n⁴-8592n³+10362n²+75600n-204864)/24, n>=9, (V. Kotesovec, 24.1.2010)

5 zebras, board nxn: (n¹⁰-90n⁸+400n⁷+2915n⁶-26880n⁵+2430n⁴+609920n³-1517496n²-4188480n+16581120)/120, n>=12, (V. Kotesovec, 26.1.2010)

Obecný vzorec není znám, ale první členy polynomu mají vždy tvar n^2k/k! - 9n^2k-2/2/(k-2)! + 20n^2k-3/(k-2)! +...

Linky na OEIS
A172137 - 2 zebras NxN
A172138 - 3 zebras NxN
A172139 - 4 zebras NxN
A172140 - 5 zebras NxN

n	2 zebras	3 zebras	4 zebras	5 zebras
2	6	4	1
3	36	84	126	126
4	112	452	1168	2032
5	276	1772	7334	20502
6	582	5596	35749	160696
7	1096	14888	137970	929880
8	1896	34640	438984	4117520
9	3072	72712	1208246	15037036
10	4726	140716	2969389	47368960
11	6972	255036	6662480	132577826
12	9936	437968	13873100	336828368
13	13756	718980	27144408	789558314
14	18582	1136092	50389581	1729320120
15	24576	1737376	89424014	3574328936
16	31912	2582576	152638280	7027309888
17	40776	3744848	251834530	13226773092
18	51366	5312620	403250693	23959787480
19	63892	7391572	628798516	41954706558
20	78576	10106736	957543164	71276149776
21	95652	13604716	1427453780	117848892710
22	115366	18056028	2087456085	190142197976

8.2) Zebras on board k x n - Zebry na šachovnici k x n

2 zebras, board 2xn: n(2n-1), =all combinations
3 zebras, board 3xn: (9n³-21n²+50n-48)/2, n>=6, (V. Kotesovec, 26.1.2010)
4 zebras, board 4xn: 4(8n⁴-48n³+202n²-471n+507)/3, n>=9, (V. Kotesovec, 26.1.2010)
5 zebras, board 5xn: 5(125n⁵-1250n⁴+7575n³-28426n²+64000n-67056)/24, n>=12, (V. Kotesovec, 26.1.2010)
6 zebras, board 6xn: (1944n⁶-27540n⁵+227070n⁴-1222555n³+4366071n²-9580580n+9925860)/30, n>=15, (V. Kotesovec, 26.1.2010)

První členy těchto vzorců mají obecně tvar (kn)^k/k! - (k-1)(9k-20)(kn)^k-1/2/k! + ...

OEIS linky:
A172221 - 3 zebras 3 X n
A172222 - 4 zebras 4 X n
A172223 - 5 zebras 5 X n
A172224 - 6 zebras 6 X n

n	2 zebras	3 zebras	4 zebras	5 zebras	6 zebras
2	6	20	70	252	924
3	15	84	406	1925	8989
4	28	200	1168	6534	37270
5	45	403	2948	20502	145233
6	66	720	6576	57710	525796
7	91	1180	13122	142312	1605490
8	120	1808	23808	308254	4136952
9	153	2631	40168	606051	9435413
10	190	3676	63996	1105332	19632414
11	231	4970	97344	1897899	37957424
12	276	6540	142516	3100250	69050898
13	325	8413	202072	4857000	119351315
14	378	10616	278828	7344010	197524064
15	435	13176	375856	10771530	314935542
16	496	16120	496484	15387310	486171662
17	561	19475	644296	21479725	729604121
18	630	23268	823132	29380900	1068003424
19	703	27526	1037088	39469835	1529198580
20	780	32276	1290516	52175530	2146783422
21	861	37545	1588024	67980110	2960869583
22	946	43360	1934476	87421950	4018886128
23	1035	49748	2334992	111098800	5376425842
24	1128	56736	2794948	139670910	7098138174
25	1225	64351	3319976	173864155	9258668837

9.1) Wazirs on board n x n - Vezíři na šachovnici n x n

Vzorce pro počet pozic neohrožujících se vezírů (skokanů [0,1]) na šachovnici n x n. Wazir is leaper [0,1].

2 wazirs, board nxn: n(n-1)(n²+n-4)/2, (C. Poisson, 1990)
3 wazirs, board nxn: (n-2)(n⁵+2n⁴-11n³-10n²+42n-12)/6, n>=2 (V. Kotesovec, 29.1.2010)
4 wazirs, board nxn: (n⁸-30n⁶+24n⁵+323n⁴-504n³-1110n²+2760n-1224)/24, n>=4, (V. Kotesovec, 29.1.2010)
5 wazirs, board nxn: (n¹⁰-50n⁸+40n⁷+995n⁶-1560n⁵-8890n⁴+21080n³+24264n²-97440n+59520)/120, n>=5, (V. Kotesovec, 29.1.2010)

Obecný vzorec není znám, ale první členy polynomu mají vždy tvar n^2k/k! - 5n^2k-2/2/(k-2)! + ...

OEIS linky:
A172225 - 2 wazirs n X n
A172226 - 3 wazirs n X n
A172227 - 4 wazirs n X n
A172228 - 5 wazirs n X n

n	2 wazirs	3 wazirs	4 wazirs	5 wazirs
2	2	0	0
3	24	22	6	1
4	96	276	405	304
5	260	1474	5024	10741
6	570	5248	31320	127960
7	1092	14690	133544	870589
8	1904	35012	446421	4197456
9	3096	74326	1258590	16005187
10	4770	144544	3126724	51439096
11	7040	262398	7042930	145085447
12	10032	450580	14669709	369074128
13	13884	739002	28658436	863338777
14	18746	1166176	53069000	1883786680
15	24780	1780714	93909924	3875953561
16	32160	2642948	159819965	7583888944
17	41072	3826670	262913874	14206566327
18	51714	5420992	419816676	25617069208
19	64296	7532326	652912510	44663199283
20	79040	10286484	991835749	75572017136

9.2) Wazirs on board k x n - Vezíři na šachovnici k x n

2 wazirs, board 2xn: 2(n-1)²
3 wazirs, board 3xn: (3n-5)(3n²-8n+8)/2, n>=2, (V. Kotesovec, 29.1.2010)
4 wazirs, board 4xn: (64n⁴-432n³+1235n²-1797n+1122)/6, n>=3, (V. Kotesovec, 29.1.2010)
5 wazirs, board 5xn: (625n⁵-5750n⁴+23535n³-54202n²+70640n-41616)/24, n>=4, (V. Kotesovec, 29.1.2010)
6 wazirs, board 6xn: 2*(486n⁶-5670n⁵+30240n⁴-95230n³+187899n²-220775n+120540)/15, n>=5, (V. Kotesovec, 29.1.2010)
7 wazirs, board 7xn: (117649n⁷-1663893n⁶+10942729n⁵-43685355n⁴+114945646n³-199980312n²+213228096n-107390880)/720, n>=6, (V. Kotesovec, 29.1.2010)

První členy těchto vzorců mají obecně tvar (kn)^k/k! - (k-1)(5k-2)*(kn)^k-1/2/k! + ...

OEIS linky:
A172229 - 3 wazirs 3 X n
A172230 - 4 wazirs 4 X n
A172231 - 5 wazirs 5 X n
A172232 - 6 wazirs 6 X n
A172234 - 7 wazirs 7 X n

n	2 wazirs	3 wazirs	4 wazirs	5 wazirs	6 wazirs	7 wazirs
2	2	2	2	2	2	2
3	8	22	61	174	504	1478
4	18	84	405	1998	10010	50726
5	32	215	1502	10741	78052	573797
6	50	442	4072	38438	368868	3581924
7	72	792	9091	107004	1280832	15516804
8	98	1292	17791	251354	3612344	52550366
9	128	1969	31660	522528	8774380	149162199
10	162	2850	52442	990816	19049692	370817854
11	200	3962	82137	1748883	37898664	831571604
12	242	5332	123001	2914894	70311824	1717417198
13	288	6987	177546	4635639	123209012	3316210152
14	338	8954	248540	7089658	205885204	6054985120
15	392	11260	339007	10490366	330502992	10545491888
16	450	13932	452227	15089178	512631720	17638773534
17	512	16997	591736	21178634	771833276	28489610297
18	578	20482	761326	29095524	1132294540	44631652698
19	648	24414	965045	39224013	1623506488	68064067456
20	722	28820	1207197	51998766	2280989952	101350519742

10) Other fairy pieces - další exokameny

Další vzorce pro rozmístění neohrožujících se exokamenů publikoval Christian Poisson v roce 1990 ve francouzském časopise Rex Multiplex. Celkem 44 vzorců (převážně vždy pro rozmístění 2-3 kamenů) vyšlo ve dvou pokračováních Rex Multiplex 29/1990, str. 829-830 a Rex Multiplex 30/1990, str. 914-915.

Nejzajímavější je tento pěkný obecný vzorec pro rozmístění dvou skokanů [x,y]
Two leapers [x,y] on chessboard n x n:

x >= y >= 0 and x+y <> 0
(n⁴-9n²+8(x+y)n-8xy)/2, for x <> y <> 0, n>=x
(n⁴-5n²+4(x+y)n-4xy)/2, for x=y or y=0, n>=x

Speciálně pro x=3 a y=2 dostaneme shodný vzorec pro 2 Zebry, pro x=1 a y=0 dostaneme shodný vzorec pro 2 Vezíry.

Jak jsem však zjistil, tento vzorec objevil už Edouard Lucas v roce 1891, když ve své knize Théorie des nombres uvádí na str.97 obecnější vzorec pro počet ohrožujících se skokanů [r,s] na šachovnici p x q
(2p - r - s)(2q - r - s) - (r - s)²
Když v tomto vzorci položíme p = q = n a uvědomíme-li si, že celkový počet kombinací 2 kamenů na šachovnici n x n je n² nad 2, dostáváme odtud pro počet neohrožujících se skokanů [r,s] výraz
n²(n²-1)/2 - (4n² - 4n(r + s) + 4rs) = (n⁴ - 9n² + 8n(r + s) - 8rs)/2, což odpovídá výše uvedenému vzorci

home page