Geometricky nejdelší uzavřená cesta krále na šachovnici 8x8
Geometrically longest king's closed tour on a 8x8 chessboard
V roce 2009 jsem se zabýval velmi zajímavým problémem geometricky nejdelší cesty krále na různých velikostech šachovnic a výsledky jsem publikoval ve své knize Využití teorie grafů v šachových úlohách na straně 51. Pro šachovnice až do rozměrů 6x6 jsem počítačem prozkoumal všechny možnosti a šlo o absolutní rekordy. Pro šachovnici 8x8 už ale nebylo možné v akceptovatelném čase prozkoumat všechny možnosti a jako rekord jsem považoval cestu dělky 10 + 54 * sqrt(2), tedy uzavřenou cestu s 10 vertikálními a 54 diagonálními tahy krále. Předpokládal jsem, že cesta délky 8 + 56 * sqrt(2) asi neexistuje.
In my book Application of Graph Theory in Chess Problems (2009), page 51, I analysed geometrically longest king's closed tour on a chessboard n x n. My program in 2009 found all solutions only up to chessboard 6x6 (proven optima). For 8x8 were not all possibilities tested and I found a closed tour of length 10 + 54 * sqrt(2), with 10 vertical and 54 diagonal moves of king.
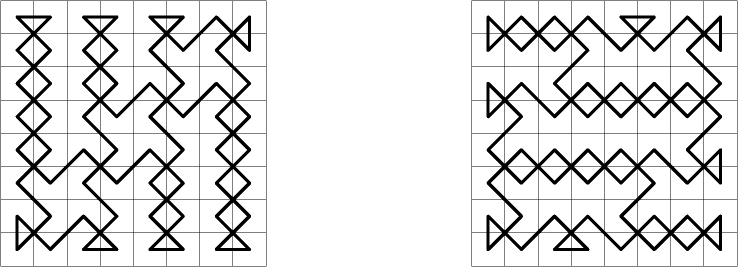
3.2.2011 mě proto překvapil e-mail, který mi poslal Zvi Mendlowitz, který takovou cestu našel. Na diagramech vidíme dvě takové možnosti uzavřených cest s 8 vertikálními a 56 diagonálními tahy krále. Velký objev!
Zvi Mendlowitz from Israel sent me 3.2.2011 geometrically longest king's tour on 8x8 board of length 8 + 56 * sqrt(2). A closed tour with 8 vertical and 56 diagonal moves of king. Great found!
Nyní si můžeme položit otázku, zda na šachovnicích sudých rozměrů n x n existuje vždy uzavřená cesta krále délky n + (n2-n) * sqrt(2), tedy s pouze n vertikálními tahy ?
Open problem: Exists for all even n on a chessboard n x n closed king's tour with only n vertical moves and length = n + (n2-n) * sqrt(2) ?
Zvi Mendlowitz wrote about it in next e-mail (5.2.2011): "I think it is easy to generalize the pattern on the left to all boards where n is divisible by 4, I don't know what about n which is not divisible by 4.
I'll try proving that for boards n x n the minimum is n orthogonal moves for n even and 2n orthogonal moves for n odd."
Současný stav geometricky nejdelších cest krále (podle rozměru šachovnice n x n) je tento:
Current state of geometrically longest king's closed tour on a 8x8 chessboard n x n:
| n=4k | n | +n(n-1)*sqrt(2) |
| n=4k+2 | n+2 | +(n-2)(n+1)*sqrt(2) |
| n=2k+1 | 2n | +n(n-2)*sqrt(2) |
home page

