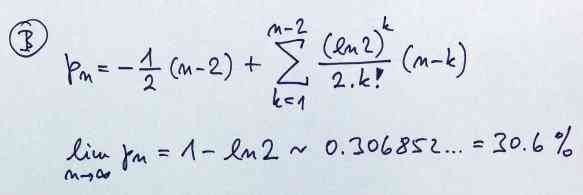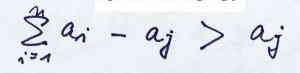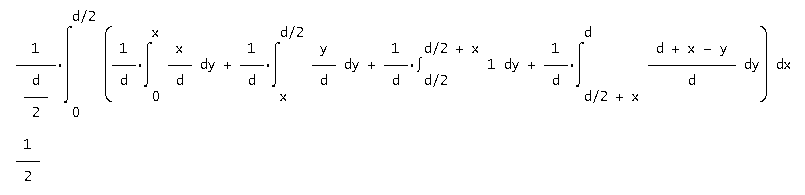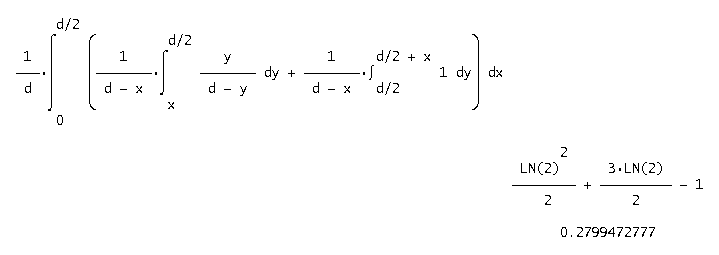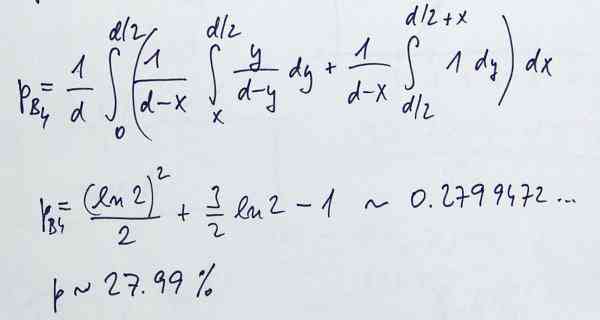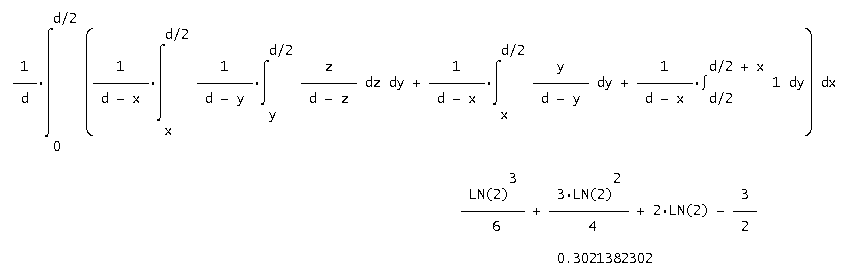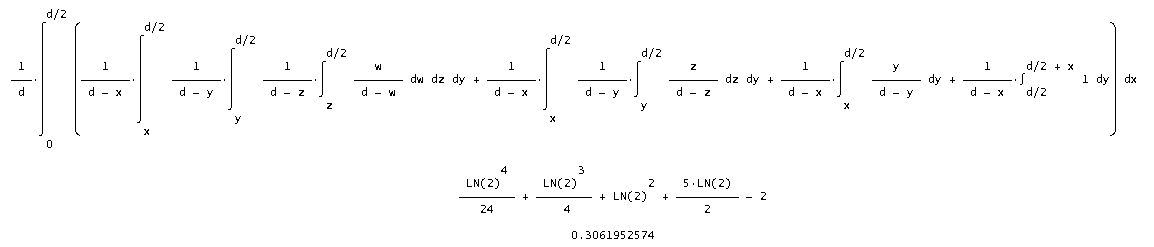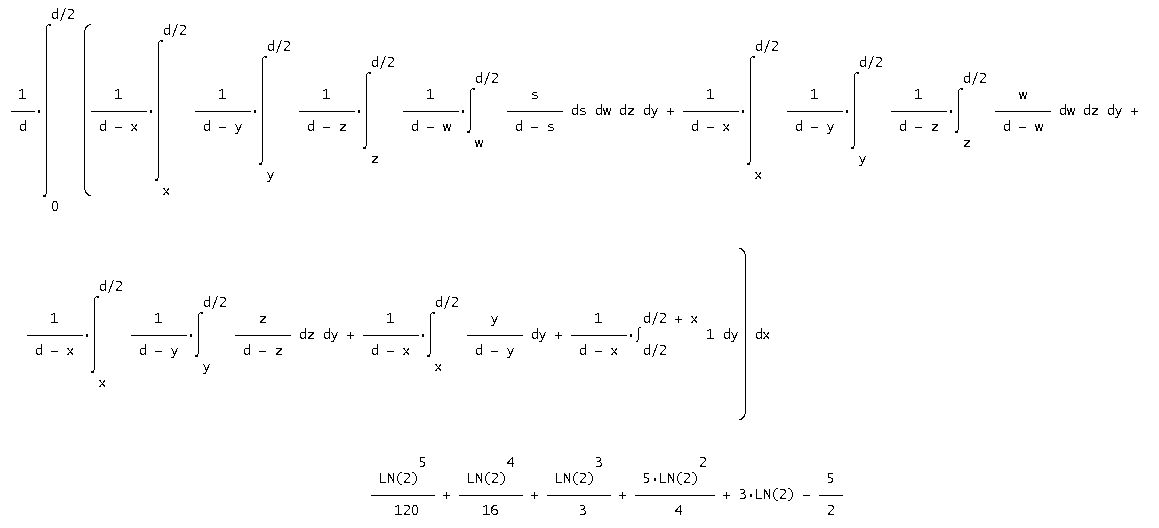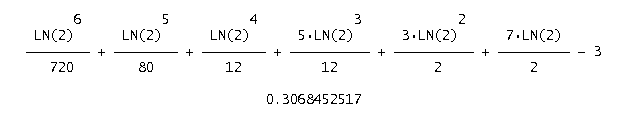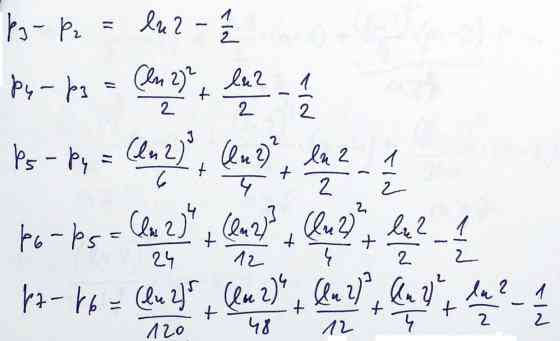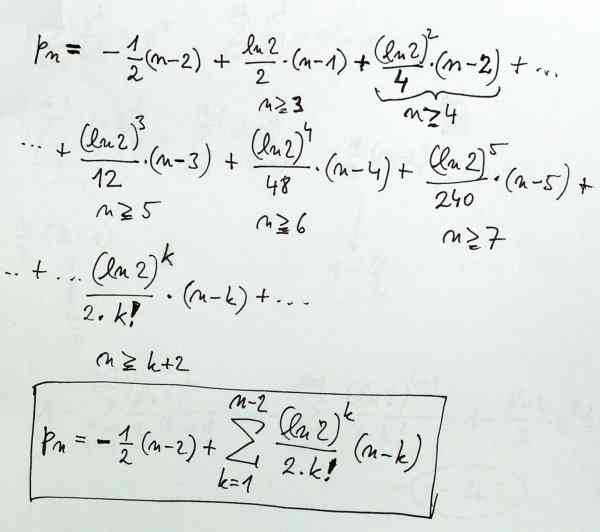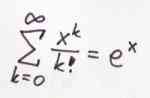Problém lámání stébla
(Václav Kotěšovec, 9.8.2007)
Fracture of grass-blade
(Summer mathematical problem by Vaclav Kotesovec)
1) Trojúhelník (Triangle)

|
|
Summary:
case A - two random fractures each on full size of grass-blade
case B - second fracture can be only between first fracture and right end of grass-blade.
How is probability that from 3 random parts is possible create a triangle ?
(see also pictures)
Solution:
in case A is probability p3 = 1/4 = 25%
in case B is probability p3 = ln 2 - 1/2 ~ 19.3 %
|
Při letním odpočinku na zahradě mě (kromě úloh šachových) napadla i jedna úloha matematická. Vezměme stéblo trávy a náhodně ho zlomíme
A) ve dvou různých bodech
B) v jednom bodě a potom znovu v bodě napravo od prvního bodu.
Jaká je pravděpodobnost v případech A a B, že z těchto 3 dílů je možné sestavit trojúhelník ?
(samozřejmě stéblo lámeme vždy tak, aby zůstalo v jedné rovině)
 | Ne vždy to jde!
|

| No possible create triangle! |
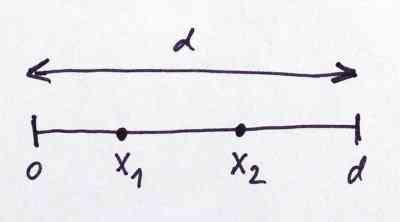
Délku stébla označme
d, souřadnice bodů zlomu označme
x1,
x2.
Body zlomu můžeme vždy uspořádat tak, že platí
0 < x
1 < x
2 < d
Podmínkou existence trojúhelníku je, aby součet délek jeho dvou stran byl vždy větší než délka strany třetí. V našem značení mají potenciální strany trojúhelníka délky:
[x
1, x
2 - x
1, d - x
2]
Dostáváme tak 3 podmínky:
1) x
1 + (x
2 - x
1) > d - x
2
2) (x
2 - x
1) + (d - x
2) > x
1
3) x
1 + (d - x
2) > x
2 - x
1
Po úpravě se výrazy zjednoduší:
1) x
2 > d/2
2) x
1 < d/2
3) x
2 - x
1 < d/2
Vidíme, že k tomu, aby šlo vytvořit trojúhelník, musí jeden z bodů zlomu ležet v levé polovině stébla,
druhý z bodů v pravé polovině stébla a vzdálenost mezi oběma body musí být menší než polovina stébla.
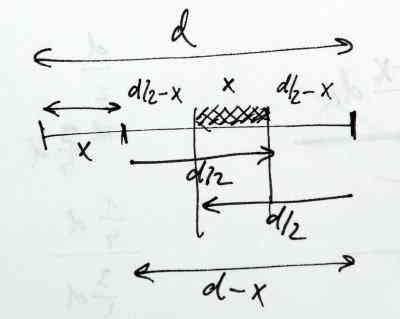
Pro zvolený bod se souřadnicí
x v levé polovině stébla dostáváme tak omezení z obou stran pro pozici druhého bodu. Délka přípustného pásma pro druhý bod zlomu je
d - x - (d/2 - x) - (d - d/2 - x) = x
Například pokud d=100 a x
1=10, pak může být x
2 pouze mezi 50 až 60, tedy v pásu délky také 10. Pro x
1=20 může být x
2 jen mezi 50 až 70, tento pás má opět délku rovnající se x
1.
Pravděpodobnost se vypočte jako počet případů, které vyhovují požadované podmínce, dělený počtem všech možných případů.
Rozlišme nyní 2 varianty této úlohy:
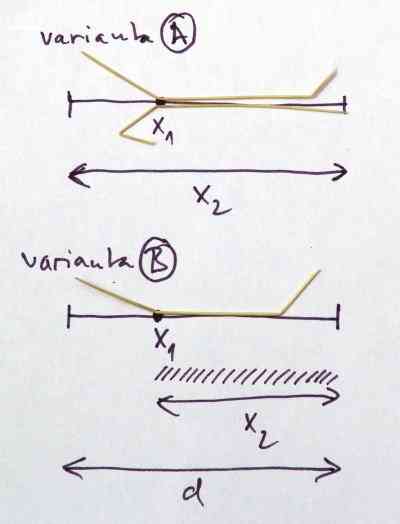
Varianta A
Po zlomení stébla v prvním bodě se souřadnicí x
1 můžeme stéblo zlomit podruhé v libovolném místě po celé délce
d, tedy napravo i nalevo od bodu se souřadnicí x
1. Celkový počet možností pro umístění bodu se souřadnicí x
2 je
d.
Při zafixovaném prvním bodu se vzdáleností
x od levého okraje je tedy pravděpodobnost pro tento jeden konkrétní bod rovna
p
x = x / d
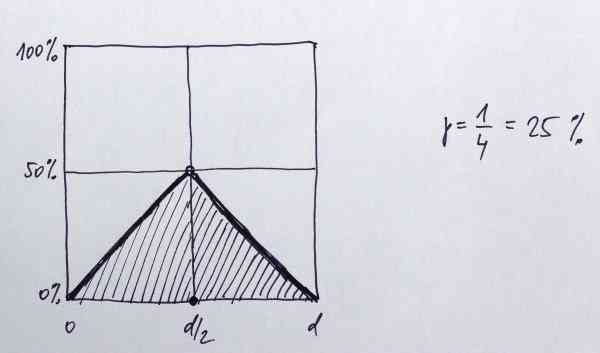
Rozložení pravděpodobnosti.
Pravděpodobnost pro body na intervalu (0,d) je symetrická kolem osy d/2.
Na určení celé plochy příznivých možností zde vystačíme s elementární matematikou.
Vidíme, že šrafovaná plocha zabírá jednu čtvrtinu z celkové plochy, tedy
(1) p3 = 1/4 = 25%
Samozřejmě i v tomto případě můžeme ale použít integrální počet (jak bude nutné ve variantě B), pravděpodobnost pro 0 <= x <= d/2 je potom
(1') p3 =
|
1
d/2
|
|
d/2

0 |
x
d
|
dx |
(1'') p
3 = 2/d*(d/2)
2/2/d = 1/4
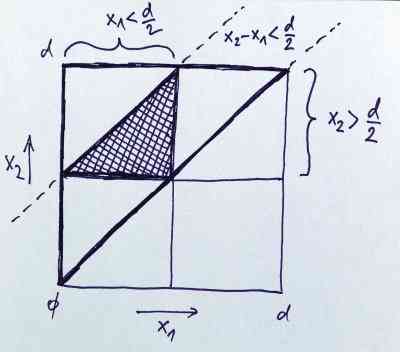
Obrázek ukazuje jiný pohled na průnik oblastí splňujících výše uvedené 3 podmínky a opět je vidět, že 1/4 plochy (šrafovaný trojúhelník) splňuje všechny 3 podmínky (je znázorněno pro x
1 < x
2, což je horní velký trojúhelník. Pro x
1 > x
2 je vše symetrické).
Varianta B
Matematicky zajímavější je druhá varianta této úlohy, kdy po zlomení stébla v prvním bodě se souřadnicí x
1
smíme druhý zlom provést už jen v části napravo od tohoto bodu, tj. x
2 > x
1.
V tomto případě zůstává počet příznivých možností pro zafixovaný bod
x stejný jako ve variantě A (roven
x), ale celkový počet všech možností je d - x.
Pravděpodobnost pro daný bod je proto pro
x
v intervalu (0,d/2) p
x = x / (d - x),
v intervalu (d/2,d) p
x = 0.
Viz obrázek.
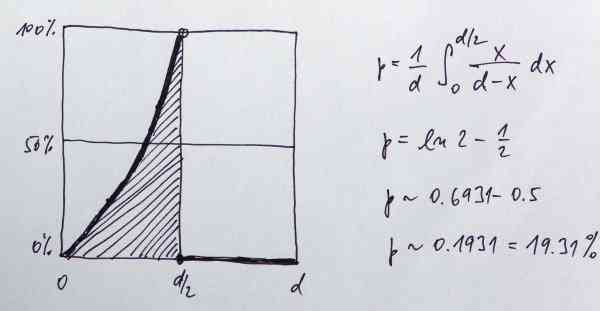
Pokud bude např. d=1000, pak budou pravděpodobnosti podle
x následující:
| x |
100 |
200 |
300 |
400 |
499 |
500 |
600 |
700 |
800 |
900 |
| px [%] |
11 |
25 |
42 |
66 |
99 |
0 |
0 |
0 |
0 |
0 |
K určení celkové pravděpodobnosti je třeba "projet" s
x přes celý interval (0,d) a k tomu už potřebujeme integrální počet. Jelikož pro x > d/2 je p=0, stačí uvažovat interval (0,d/2) s váhou 1/2 a součet všech hodnot vydělit délkou tohoto intervalu d/2.
| (2) |
p3 =
|
1/2
d/2
|
|
d/2

0 |
x
d-x
|
dx |
| (2') |
p3 =
|
1
d
|
|
d/2

0 |
x
d-x
|
dx |
(3) p
3 = 1/d * (d ln 2 - d/2)
(3')
p3 = ln 2 - 1/2
Numericky je:
p3 ~ 0.69314... - 0.5 = 0.19314... ~
19.3 %
Jak se dalo očekávat, pravděpodobnost nezávisí na délce stébla (ani v A ani v B).
Ze zdánlivě jednoduché úlohy vznikl poměrně netriviální problém, který má velmi elegantní řešení.
Koho by napadlo, že v jednom stéble trávy je "ukryt" přirozený logaritmus 2 ?
2) N-úhelník (Polygon)
Generally, for n-angle polygon is probability
in case A

in case B
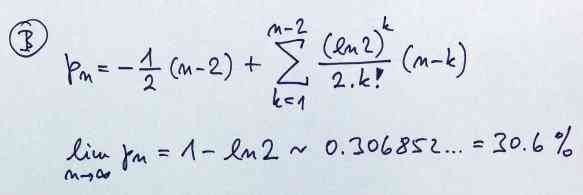
Limit for
n to infinity is 1 - ln 2 ~ 30.6%
Úlohu jsem nakonec zobecnil na hledání pravděpodobnosti, zda lze uvedenými postupy vytvořit n-úhelník. Zajímavé je též hledání limity těchto pravděpodobností pro
n jdoucí do nekonečna.
Pro n-úhelník se stranami a
1, a
2, ... , a
n, kde součet těchto stran je roven
d, musí platit pro každou ze stran, že součet délek ostatních stran je vždy větší než délka této strany. Jelikož ale víme, že součet všech stran (obvod n-úhelníka) je
d, můžeme tyto podmínky zjednodušit na
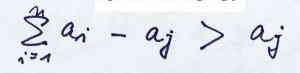
d - a
j > a
j
z čehož vyplývá
(4)
aj < d/2
pro všechna
j od 1 do n.
Problém vytváření n-úhelníku lámáním stébla je tedy ekvivalentní tomu, když budeme náhodně "střílet" do oblasti délky
d, že po
n výstřelech nebude mezi body existovat mezera délky
alespoň d/2.
Vzhledem k celkové délce
d může taková mezera délky >=d/2 existovat maximálně jedna.
Podobně jako v případě trojúhelníku rozlišíme opět varianty A a B.
Zabývejme se nejprve
čtyřúhelníkem (tetragon). Mějme 3 zlomové body se souřadnicemi
x,
y,
z.
Ve variantě A musíme po umístění bodu
x do intervalu (0,d/2) rozlišit celkem 4 možnosti pro umístění bodu
y.
(Pro
x se stačí zabývat jen polovičním intervalem, protože ve druhé polovině je vše symetrické a pravděpodobnost je tedy shodná)

na obrázku je příslušná suboblast, ve které se pohybuje bod
y, označena vždy tučnou čarou.
Pokud nyní uvažujeme třetí zlom na stéble, tedy pohybujeme bodem
z v intervalu (0,d), vznikne mezera mezi body větší nebo rovna než d/2 v částech označených nulami. Naopak v částech označených 1 jsou všechny mezery mezi body (i okraji) menší než d/2. Dílčí pravděpodobnosti jsou potom
| interval y | pravděpodobnost |
| (0,x) | x/d |
| (x,d/2) | y/d |
| (d/2,d/2+x) | 1 |
| (d/2+x,d) | (d+x-y)/d |
Celkovou pravděpodobnost pak určíme jako součet dílčích integrálů takto:
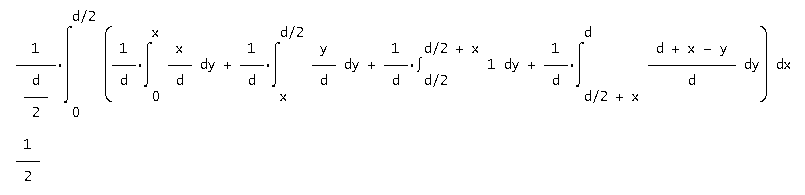
Pro vyřešení jsem použil program Derive (který umí podobné výrazy zjednodušovat na symbolické úrovni!).
Výsledná pravděpodobnost pro 4-úhelník je
(5)
p4 = 1/2
Pro víceúhelníky je použití stejného postupu sice možné, ale množství případů (různých subintervalů) se neúměrně zvyšuje. Postupoval jsem proto tak, že jsem napsal jednoduchý program, který pomocí náhodných čísel generuje náhodné rozložení bodů v intervalu (0,1) (d=1) a počítá příznivé případy. Nechal jsem projet 10000000 cyklů a zde jsou výsledky:
| estimated | estimated | 1 - n/2n-1 | exact |
| n | varianta A | varianta B | varianta A | varianta B |
| 3 | 24.9988 % | 19.3172 % | 25.000000 % | 19.31471805 % |
| 4 | 50.0111 % | 27.9821 % | 50.000000 % | 27.99472777 % |
| 5 | 68.7337 % | 30.2104 % | 68.750000 % | 30.21382302 % |
| 6 | 81.2531 % | 30.6216 % | 81.250000 % | 30.61952574 % |
| 7 | 89.0685 % | 30.6679 % | 89.062500 % | 30.67765758 % |
| 8 | 93.7449 % | 30.6883 % | 93.750000 % | 30.68452517 % |
| 9 | 96.4771 % | 30.6924 % | 96.484375 % | 30.68521626 % |
| 10 | 98.0427 % | 30.6950 % | 98.046875 % | 30.68527687 % |
| inf | | | 100 % | 30.68528193 % |
(First two columns in table was created by special computer program with help of random number generator, second two columns are exact results)
Tento postup je také dobrý k numerickému ověření analytických výsledků (viz sloupce vpravo).
Analýzou výstupů jsem zjistil (a následně ověřil i pro další
n), že pro případ A platí
(6)
pn = 1 - n/2n-1

Limita pro
n jdoucí do nekonečna je rovna 1 a odpovídá stočení hladkého stébla spojením jeho 2 konců (což jde vždy).
Varianta B
Pokud můžeme stéblo lámat pouze vpravo od předchozích zlomů, je počet nutných subintervalů menší a problém se mi podařilo vyřešit i analyticky. Následně jsem (podle numerických výsledků z programu) ověřil, že analytické výsledky jsou správné.
Začneme opět
čtyřúhelníkem (tetragon)

Označení jednotlivých úseků je shodné jako na předchozím obrázku (pro případ A). Opět musíme rozlišit několik možností umístění bodu
y do intervalů. Bod
z nyní umísťujeme do intervalu (y,d) a dílčí pravděpodobnosti jsou:
| interval y | pravděpodobnost |
| (x,d/2) | y/(d-y) |
| (d/2,d/2+x) | 1 |
| (d/2+x,d) | 0 |
Celková pravděpodobnost je potom dána integrálem
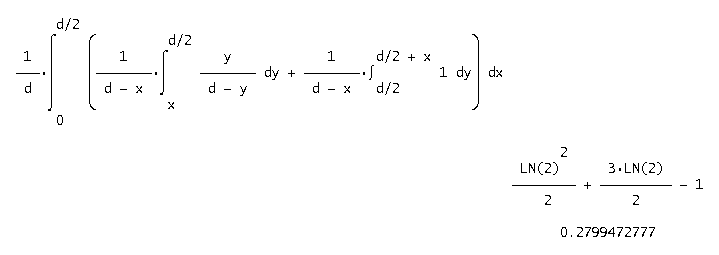
Vyřešení programem Derive dává výsledek
(7)
p4 = (ln 2)2/2 + 3 * ln 2 /2 - 1
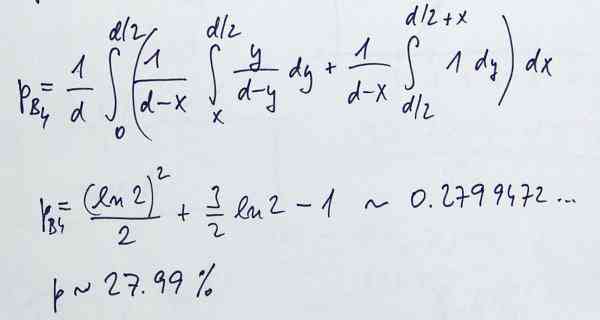
Pro 5-úhelník je pravděpodobnost
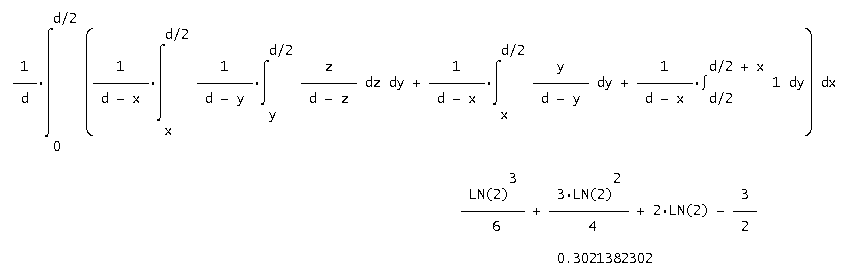
Pro 6-úhelník je pravděpodobnost
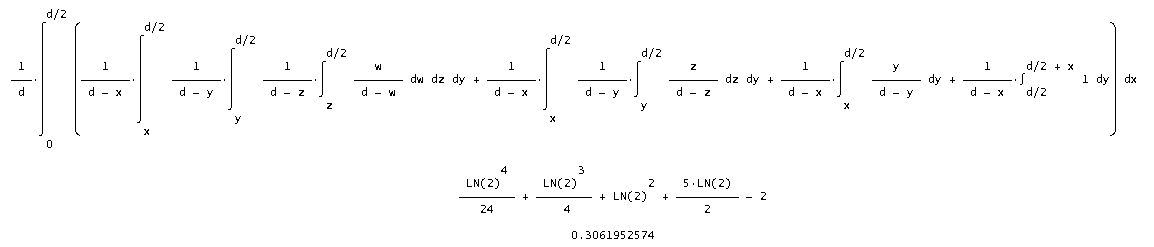
Pro 7-úhelník je pravděpodobnost (na screenshotu z programu Derive integrál pokračuje na další řádce)
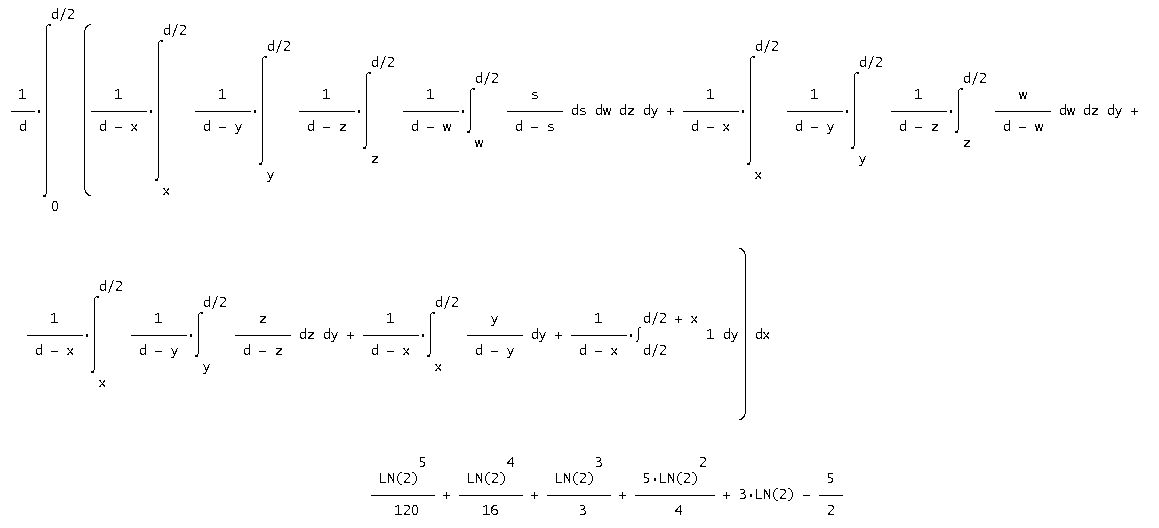
Pro 8-úhelník je pravděpodobnost
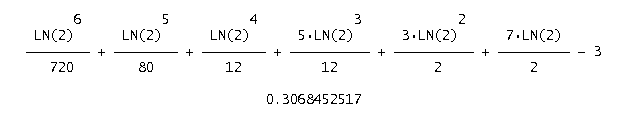
Pokud takto pokračujeme pro další n, dostáváme tyto pravděpodobnosti
| n | pn | numericky |
| 3 | (ln 2)-1/2 | 0.1931471805 |
| 4 | (ln 2)2/2+3*(ln 2)/2-1 | 0.2799472777 |
| 5 | (ln 2)3/6+3*(ln 2)2/4+2*(ln 2)-3/2 | 0.3021382302 |
| 6 | (ln 2)4/24+(ln 2)3/4+(ln 2)2+5*(ln 2)/2-2 | 0.3061952574 |
| 7 | (ln 2)5/120+(ln 2)4/16+(ln 2)3/3+5*(ln 2)2/4+3*(ln 2)-5/2 | 0.3067765758 |
| 8 | (ln 2)6/720+(ln 2)5/80+(ln 2)4/12+5*(ln 2)3/12+3*(ln 2)2/2+7*(ln 2)/2-3 | 0.3068452517 |
(These results were discovered with analytical method and solved by program Derive)
Porovnal jsem nyní tyto přesné výsledky s odhady generovanými náhodnými čísly a je vidět, že výsledky jsou shodné. Nejzajímavější část řešení problému však byla ještě přede mnou. Dal jsem si za cíl odvodit obecný vzorec a pomocí něho pak určit limitu když jde
n do nekonečna. Vytvořil jsem si nejprve diference získaných pravděpodobností:
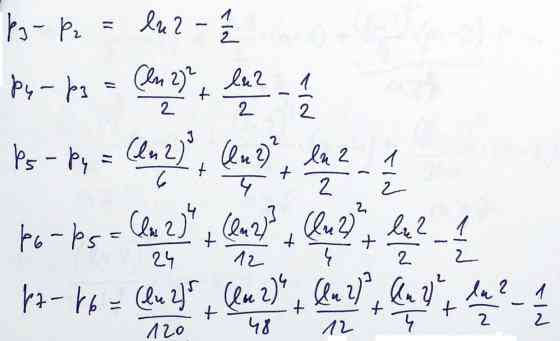
Z těchto výsledků jsem odvodil
obecný vzorec
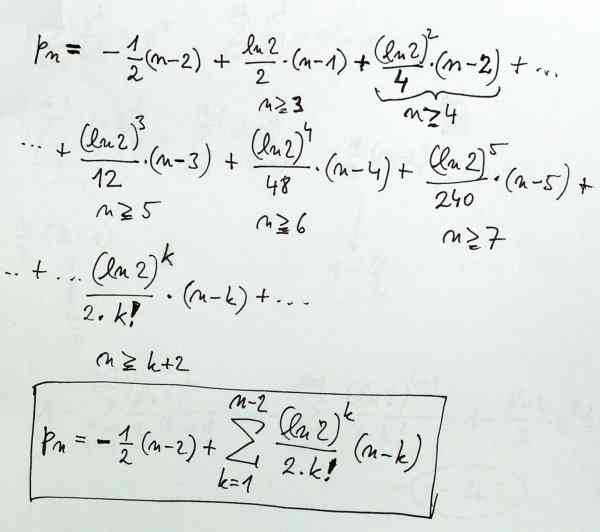
Odtud jde už vypočítat limitu této pravděpodobnosti pro
n jdoucí do nekonečna. Pomůže nám znalost Taylorova rozvoje
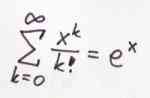
Výraz pro p
n nejprve mírně upravíme a sečteme jednotlivé sumy.

Členy s n/2 se vyruší a zůstane překvapivě jednoduchý výsledek
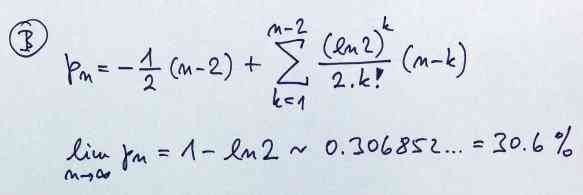
(8) pro n jdoucí k nekonečnu
lim pn = 1 - ln 2 ~ 1 - 0.693... = 0.3068528193...
Numericky tato hodnota odpovídá výsledkům získaným generátorem náhodných čísel.
Jak je vidět, přirozený logaritmus 2 neopustil stéblo trávy ani v nekonečnu...