Alfabetický šach (dále jen ABC šach) vymyslel v roce 1985 francouzský skladatel Romeo Bédoni (viz Rex Multiplex 15-16/1985, str. 508) původně s úmyslem dosáhnout jednoznačnosti řešení zejména u sériovotahových úloh. Časem se však ukázalo, že možnosti ABC šachu v šachové kompozici jsou mnohem širší a že obsahuje řadu specifických motívů, které umožňují realizovat originální náměty.

Alphabetic chess was invented in 1985 by the French composer Romeo Bédoni (see Rex Multiplex 15-16/1985, p. 508), originally with the intention of achieving unambiguity of solution, especially for serial move problems. Over time, however, it became apparent that the possibilities of the ABC in chess composition were much wider and that it contained a number of specific motifs that allowed original themes to be realised.

Definice: Alfabetický šach (alphabétiques, Alphabet-chess) Obě strany jsou povinny hrát kamenem, který je první z hlediska algebraické notace v pořadí a1-a8, b1-b8, c1-c8, atd. Pokud tento kámen nemůže táhnout, musí hrát druhým v pořadí atd.

Definition: Alphabet chess (ABC chess, Alphabétiques) - Each move of either side must be by the piece occupying the first square in the order of a1, a2, a3, ... , b1, b2, b3, ..., c1, c2, c3, ... etc., which is able to make a legal move. Castling is permitted if the King has the right to make a legal alphabetical move, provided the usual other rules for that move are obeyed.

Od té doby vznikla řada úloh (v databázi WinChloe je nyní 3094 úloh v ABC šachu a v PDB 3201 úloh). Nikoho zatím ale ještě nenapadlo prozkoumat teorii koncovek v ABC šachu. S materiálem K+D-K můžeme v PDB najít jen jednu osmitažku P1251945. Je však tato koncovka vyhraná z obecné pozice tak jako v ortodoxním šachu ?

Since then a number of problems have been created (there are now 3094 problems in the WinChloe database in ABC chess and 3201 problems in PDB). However, no one has yet thought to investigate the theory of endings in ABC chess. With the K+Q-K material, we can find only one eightmover in the PDB P1251945. But is this ending won from a general position as in orthodox chess ?

Odpověď na tuto otázku je, že v ABC šachu král s dámou vyhrávají proti samotnému králi jen ve 46% pozic. Nejdelší výhra má 62 tahů! Právě překvapivá složitost této zdánlivě jednoduché koncovky mě vedla k napsání tohoto článku.

The answer to this question is that in ABC chess the king and queen win against a bare king in only 46% of positions. The longest win has 62 moves! It was the surprising complexity of this seemingly simple ending that led me to write this article.

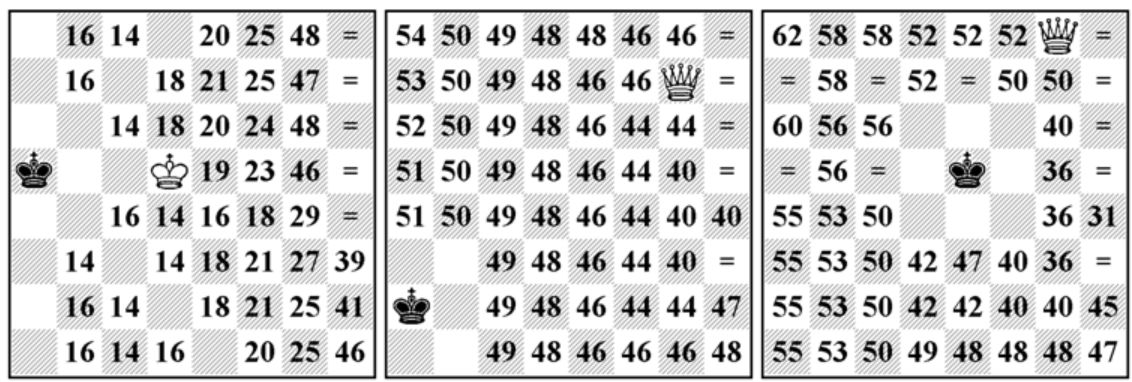
Vzhledem definici ABC šachu je třeba si uvědomit, že pohyblivost kamenů se směrem do prava k h-sloupci postupně zmenšuje. Pokud je např. bílá dáma na poli h8, stává se nepohyblivou (neztrácí však působnost), protože ji bílý král nemůže svými tahy již vrátit do hry (kdyby byla dáma na poli h7, může jí král vrátit do hry tahem na h8, pak se ovšem dostane do stejné situace král). To ovšem neplatí, pokud má jedna ze stran jen jeden kámen.

Možnosti této koncovky ilustrují následující diagramy, ve kterých jsou vždy 2 kameny zafixované a čísla určují počet tahů do matu, pokud na toto pole umístíme třetí z kamenů. Pokud je na poli znak "=" je taková koncovka remízová, při umístění kamene na prázdné pole by byla pozice ilegální.

Given the definition of ABC chess, it is important to note that the movement of the pieces gradually decreases to the right towards the h-column. For example, if the white queen is on the h8 square, it cannot make a move (but it does not lose its ability to check) because only the white king has to move (if the queen was on the h7 square and the king moved to the h8 square, the queen could move again, but then the king is now in the same situation). This is not the case, however, if either side has only one piece.

Matový postup u #62 (jako vícetažka má ovšem taková úloha řadu duálů, jednoznačné tahy jsou označeny vykřičníkem), uvedena je jedna z možných variant.

The solution in 62 moves is as follows (as a moremover, however, such a problem has a number of duals). One of the possible variants is given. Unambiguous moves are marked with an exclamation mark.

Ještě mohu doplnit, že koncovky K+V-K a K+S+J-K jsou v ABC šachu z obecné pozice remízové, silnější strana vyhraje jen v některých pozicích, kde je černý král na okraji šachovnice a bílý král poblíž.

I may add that the endings king + rook against king and king + bishop + knight againts king are generally drawn in ABC chess, the stronger side wins only in some positions where the black king is on the edge of the board and the white king is nearby.