Pod DOSem bývalo vše jednoduché a chování programů bylo systémově téměř nezávislé. Jakmile se začala zvětšovat kapacita pamětí, bylo možné implementovat nový algoritmus, tzv. hashování. U programů, které jej používají, je doba řešení šachových úloh výrazně závislá na velikosti paměti, kterou má program v danou chvíli k dispozici. Je zajímavé s touto velikostí experimentovat a porovnávat časy řešení.
V případě programu POPEYE jsou dokonce nutné 3 verze programu pro různé operační systémy. Smysl mají PYWIN98.exe pod Win98/WinME a PYWIN32.exe pod WinXP/W2k. Více o tom v sekci programs. Parametrem maxmem se dá velikost maximální použitelné paměti definovat. Nutnou podmínkou je samozřejmě existence odpovídající fyzické paměti RAM v počítači. Předdefinovaná hodnota 2MB je velmi malá. Při 1GB RAM používám obvykle 900MB (dobré je nechat určitou rezervu pro ostatní programy). Znak M je nutno zadat velkým písmenem, například
pywin32.exe -maxmem 900M problems.py
Pod WinXP je skvělý "Windows task manager" (je také pod W2k, ale bez grafu "Networking"), startuje se po ctrl/alt/del. Často používám zobrazení využití CPU a paměti pro jednotlivé tasky (zejména pro POPEYE to umožňuje zjistit aktuální spotřebu paměti!).
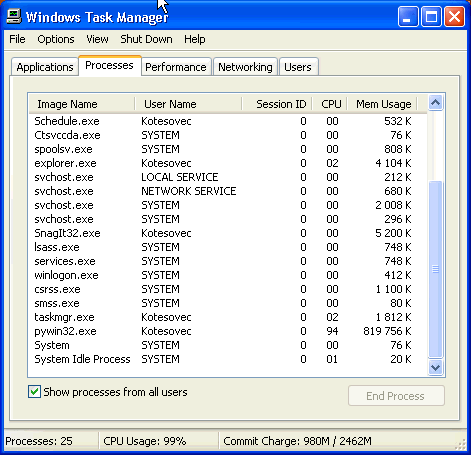
Tato analýza umožňuje také zjistit jak programy uvnitř fungují. POPEYE zde najdeme jako pywin32.exe, ALYBADIX nebo VKSACH jako NTVDM.EXE (NT Virtual Dos Machine). Zatímco ALYBADIX si na začátku vyhradí maximální paměť, která mu zůstává přidělena až do ukončení programu, POPEYE požadují paměť od systému postupně a s každou novou úlohou ji celou uvolní.
Při sledování narůstající paměti vidíme, kolik paměti je skutečně potřeba. Samozřejmě nejlepších časů řešení je dosaženo tehdy, pokud celá paměť stačí a není nutný tzv."pruning", kdy se po zaplnění část paměti musí uvolnit.
Když v menu "Processes" klikneme pravým tlačítkem myši na daný task, je možné (kromě abortování) také zvolit prioritu. Toho lze využít například takto: mám puštěné POPEYE s řešením na několik hodin. Pokud spustím jiný program bude čas CPU sdílen - obvykle 50:50, ale také to ještě závisí na tom, která úloha je na popředí (foreground) a která v pozadí (background), někdy to může být pro 2 tasky i 33:66. Občas jsou některé programy napsané tak nešťastně, že skoro vůbec nejedou, pokud jiný program využívá CPU na 100%.
Jako nejlepší řešení se ukázalo spouštět řešení šachových úloh s prioritou Below normal, potom řešení jede na pozadí a nezdržuje ostatní programy. Pokud spustíme jiný program, má předdefinovanou prioritu "Normal" a běžící řešení bude v tuto chvíli odstaveno a pojede jen v době, kdy druhý program bude na něco čekat. Po skončení urgentního programu bude řešení pokračovat dál se 100% využitím CPU. Samozřejmě to předpokládá, že spoustěné programy nevyužívají 100% CPU, protože pak by bylo řešení trvale odstaveno.
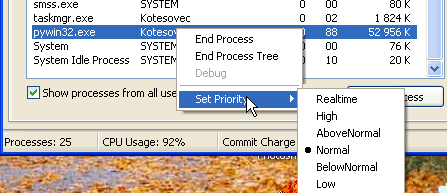
Pokud se nám nechce vždy prioritu znovu nastavovat, lze si vytvořit batch file s definovanou prioritou takto (vyzkoušeno pod Windows XP):
start /BELOWNORMAL pywin32.exe
Již přes 15 let mám zabudovanou ve VKSACHu možnost uložení RST souboru, pak je možné vypnout počítač a pokračovat dále od místa přerušení.
Funkce "Hibernate" dělá toto pro celý počítač. Uloží obsah paměti i registrů do souboru hiberfil.sys, jehož velikost je o málo větší než velikost paměti RAM v počítači. Tuto funkci musí podporovat hardware, ale v novějších počítačích je tato podmínka splněna.
Hibernace funguje pod W2k a WinXP (nefunguje pod Win98/ME). Klikneme na "Turn off computer" a (pod WinXP) je nutno podržet klávesu SHIFT a kliknout na "Hibernate". Pod WinXP trvá uložení paměti 1GB asi 2 minuty (vylepšení proti W2k, kde trvalo až 10 minut). Počítač se potom sám vypne. Po zapnutí se načte celá paměť a pokračuje se od místa hibernování (pod oběma systémy Win2k/XP trvá pro 1GB shodně 5-10 minut)

Tuto funkci samozřejmě využijeme při nutnosti vypnout počítač, když máme rozjeté nějaké dlouhé řešení. Nedávno jsem ji využil takto. Měl jsem spuštěný Alybadix asi 5 hodin a vypadla elektrika. UPS (záložní zdroj) vydrží tak 30 minut (pokud bych vypnul monitor), raději jsem dal Hibernate, vše se během asi 2 minut uložilo a počítač se vypnul. Proud naběhl asi až za hodinu. Po restartu pokračovalo řešení od místa uložení a za další asi 2 hodiny úspěšně skončilo.
Pod systémy W2k a bohužel i WinXP jsem objevil jednu zajímavou chybu. Pokud máme spuštěný DOSový program (ALYBADIX, VKSACH, POPEYE), tak po hibernaci jde čas rychleji. Závisí to na době, jak dlouho byl počítač vypnutý. Tato chyba nemá vliv na správnost řešení, ale zobrazený celkový čas řešení je v tomto případě ve skutečnosti značně menší než uvedený. Jako by se za dobu mezi hibernací a novým zapnutím počítače nashromáždily neobsloužené "timer ticky" a systém je pak postupně zpracovává. Ze začátku jde čas asi až 3x rychleji, po určité době (až několik hodin) se čas vyrovná. Chybu mám ověřenou i z jiných počítačů a uživatelským softwarem ji nelze ovlivnit. Pokud DOSový program po zapnutí počítače ukončíme a bezprostředně po tom znovu spustíme, jde čas normálně.
Ještě je nutno poznamenat, že hibernace nenahradí zcela RST soubor. Ten se vytváří automaticky jednou za hodinu nebo po ručním přerušení řešení. Při ztuhnutí počítače (crash) je možno pomocí RST souboru pokračovat od posledního bodu uložení. Žádný jiný program než VKSACH toto neumí.
V programu POPEYE je možné použít "opt StartZugnummer N" ("opt StartMoveNumber N"), kde N je číslo počátečního tahu-1 (zjistí se podle "opt Zugnummern"). Lépe by se to mělo označovat jako počet vynechaných tahů, když dám "opt StartZugnummer 4", začne se od tahu číslo 5. To může ale představovat značnou časovou ztrátu, nemluvě o tom, že je zcela ztracena paměť pro hashování a musí se vytvářet znovu.
ALYBADIX umožňuje pouze změnit pořadí probíraných kamenů v menu "Queue and movability", což může v nouzi trochu pomoci.
ALYBADIX řeší n-tahové úlohy postupně od 1., 2., ... , n-1 tahu, z toho lze výsledný čas poměrně dobře odhadnout. Tento postup lze k odhadu samozřejmě použít i u jiných programů.
Pokud řešíme programem POPEYE náročné úlohy, jejichž doba řešení se dá těžko odhadnout, je dobré používat parametr
opt Zugnummern
(v anglické verzi "opt MoveNumbers")
který po prozkoumání každého prvního tahu vypíše řádku s časovou informací. Podle toho je hrubý odhad možný. Je třeba si ale uvědomit, že při použití hashování trvají nejdéle první tahy a postupně se řešení zrychluje, někdy velmi výrazně. Takže skutečná doba řešení je značně optimističtější než násobek počtu prvních tahů a času po prvním z nich. Dokumentuje to následující příklad
čas ve vteřinách / číslo tahu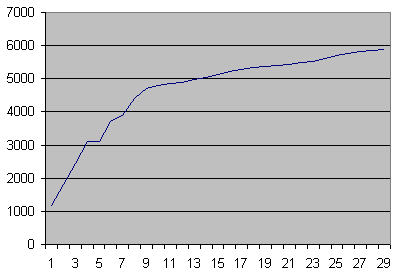
Popeye WINDOWS-32Bit-Version 3.75 (900 MB)
Rudolf QUECK
2. Pr. Memorial T.R. Dawson
+---a---b---c---d---e---f---g---h---+
| |
8 . . . . . -D . -T 8
| |
7 . K . . . . . . 7
| |
6 -B . . . . . . . 6
| |
5 . . . . . . . . 5
| |
4 . . . . . . . . 4
| |
3 B . . . . . . . 3
| |
2 . -K . . . . . . 2
| |
1 . . . . . D . T 1
| |
+---a---b---c---d---e---f---g---h---+
h==4 4 + 4
Gitterschach
1 (Kb2-c2 Zeit = 19:50.221 m:s)
2 (Kb2-b3 Zeit = 30:18.985 m:s)
3 (Kb2*a3 Zeit = 40:51.845 m:s)
4 (Kb2-c3 Zeit = 51:50.813 m:s)
5 (Kb2-c1 Zeit = 51:50.813 m:s)
6 (Df8*a3 Zeit = 1:02:00 h:m:s)
7 (Df8-b4 + Zeit = 1:05:05 h:m:s)
8 (Df8-c5 Zeit = 1:13:33 h:m:s)
9 (Df8-d6 Zeit = 1:18:17 h:m:s)
10 (Df8-h6 Zeit = 1:19:58 h:m:s)
11 (Df8-g7 + Zeit = 1:20:50 h:m:s)
12 (Df8*f1 Zeit = 1:21:38 h:m:s)
13 (Df8-f2 Zeit = 1:22:58 h:m:s)
14 (Df8-f3 + Zeit = 1:23:54 h:m:s)
15 (Df8-f4 Zeit = 1:25:27 h:m:s)
1.Df8-f5 Df1-f4 2.Th8-a8 Th1-a1 3.Df5-b1 Df4-b8 4.Kb2-c1 + Kb7-c8 ==
16 (Df8-f5 Zeit = 1:27:04 h:m:s)
17 (Df8-f6 Zeit = 1:27:51 h:m:s)
18 (Df8-a8 Zeit = 1:29:08 h:m:s)
19 (Df8-b8 Zeit = 1:29:45 h:m:s)
20 (Df8-c8 + Zeit = 1:29:56 h:m:s)
21 (Df8-d8 Zeit = 1:30:41 h:m:s)
22 (Df8-g8 Zeit = 1:31:44 h:m:s)
23 (Th8*h1 Zeit = 1:32:16 h:m:s)
24 (Th8-h2 Zeit = 1:33:30 h:m:s)
25 (Th8-h3 Zeit = 1:35:14 h:m:s)
26 (Th8-h4 Zeit = 1:36:07 h:m:s)
27 (Th8-h5 Zeit = 1:36:58 h:m:s)
28 (Th8-h6 Zeit = 1:37:24 h:m:s)
Loesung beendet. Zeit = 1:38:06 h:m:s