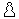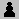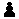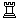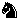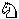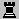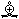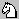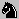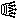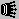Only G-promotions in fairy chess
Exoúlohy, ve kterých jsou všechny tahy spojeny s proměnou na cvrčky
(Vaclav Kotesovec, 10.7.2006)(new problems G6A and G11A added 26.7.2006, G6B added 24.11.2006, G12 added 30.12.2006, G13 added 6.1.2007, G14 added 31.1.2007, G6G added 21.4.2007, G16 added 10.7.2007, G13A added 21.7.2007, G6C and G6D added 10.10.2007, G6E and G6F added 11.10.2007, G6H and G15 added 17.10.2007, G6I,G6J,G6K added 10.11.2007, G17 added 28.3.2008, G5A added 9.5.2008, G6Av added 19.10.2008, updated 17.2.2011)
|
G1 - Wilhelm Kramer Aachener Anzeiger 1930
|
Pomocné maty a paty1.d1G g8G 2.e1G a8G#Prototypem tohoto tématu je určitě úloha G1 [4/4], která přináší 4 sekvenční proměny na cvrčky. V této úloze staví bílý cvrčka g8 aby jím pokryl pole g1, k vytvoření matové sítě mu však zbývá pokrýt pole h2. Toho lze dosáhnout cvrčkem a2 pokud bude "vyčištěna" jeho linie k tomuto poli. Proto musí černý proměnit oba pěšce, jde o to na co a v jakém pořadí. Ortodoxní kameny buď dávají při proměnách šach nebo mohou následným tahem vstoupit do linie b7-f3, takže jedinou možností jsou proměny na 2 černé cvrčky. Pořadí proměn je dáno tím, že proměna pěšce e2 v prvním tahu by byla spojena se šachem a je možná až po odchodu pěšce z d2. Matí pěšec a7, když se promění na cvrčka a nyní cvrček g2 nemá kam odskočit. Velmi ekonomicky zpracováno a je překvapující, že k cíli nevedou např. proměny na bílé dámy. Jediným technickým kamenem sloužícím k udržení korektnosti je pěšec h5. |
|
G2 - Theodor Steudel Problemkiste 1989
|
1.g:h1G+ b8G 2.c1G g8G= Jiné (patové) schéma vymyslel T.Steudel v úloze G2 [4/4]. |
|
G3 - Daniel Papack 3.Pr. harmonie 2002
|
1.f:e1G c:b8G 2.b:a1G+ g8G 3.c1G b:a8G= K napsání tohoto článku mě inspirovala geniální úloha G3 [6/6] s 6 sekvenčními proměnami. Proč až 3.cena ? Já bych jí dal bez váhání 1.cenu! (1. a 2.cena v této soutěži nebyly lepší...) |
|
G4 - K.Wenda + H.Bernleitner 3.Lob e.a. The Problemist 1996
|
1.a1G Tb1 2.c:b1G(Th1) T:d1(Sg8)+ 3.e:d1G(Th1) a:b8G(Th8) 4.g:h1G g:h8G= Zejměna Klaus Wenda se pokoušel skládat úlohy s dokonce ještě více sekvenčními proměnami, ale v G4 [6/8] je pouze 6 proměn z 8 tahů |
|
G5 - Klaus Wenda Problemkiste 1996
|
1.h:g1G c8G 2.g:h1G Gh8 3.e:f1G e8G 4.f:e1G d8G= a v úloze G5 [7/8] je 7/8 proměn. |
|
G5A - Unto Heinonen 7094 Problemkiste 176/2008
|
1.e1G h8G 2.Gee8 e:f8G 3.b:a1G c:d8G 4.c1G Th7= [6/8] Alybadix testoval 55 hodin 28 minut. (added 9.5.2008) |
|
G6 - Klaus Wenda Rochade Europa 1997v
|
Poznámka: Klaus Wenda pak také složil úlohu G6 s 8/8 proměnami s použitím věžových lionů, v této skladbě se mi ale podařilo najít vedlejší řešení. I když typem proměn úloha nezapadá do původního záměru tohoto článku, uvádím ji zde na doplnění a také proto, že nekorektnost pravděpodobně zatím nebyla nikde publikována (pouze ve WinChloe databázi). 1.c:d1TL(Lf1) g:h8TL(Dd8) 2.e:f1TL c:d8TL 3.g:h1TL(Sb1) e:f8TL(Sb8) 4.a:b1TL a:b8TL= cook 1.c:d1TL(Lf1) a8TL 2.e1TL TL:g2 3.TLa1 e:f8D(Sb8) 4.TLd8 c:b8D= |
|
G6A - Klaus Wenda F2486 The Problemist 7/2006
|
1.c:d1LI(Lf1) a:b8LI(Dd8) 2.e:f1LI c:d8LI 3.g:h1LI(Sb1) e:f8LI(Th8) 4.a:b1LI g:h8LI= Úloha G6A [8/8] vznikla zřejmě jako reakce na tento článek a je pokusem o opravu nekorektní G6. Moje předpověď, že tato úloha bude nekorektní, se ukázala jako správná, Unto Heinonen našel toto vedlejší řešení: cook 1.ed1LI(Lf1) ab8LI(Dd8) 2.gf1LI cd8LI 3.c1T ef8T(Th8) 4.LI:f8(Ta1) gh8LI= (added 26.7.2006, updated 17.10.2007) |
|
G6Av - Klaus Wenda The Problemist Mar. 2009 (final version of 2486)
|
1.c:d1LI(Lf1) a:b8G(Dd8) 2.e:f1LI c:d8LI 3.g:h1G(Sb1) e:f8LI(Th8) 4.a:b1G g:h8G= [8/8] Kombinace 4 cvrčkových a 4 lionových proměn. Úlohu jsem testoval Alybadixem 156 hodin 36 minut a je korektní za podmínky, že se pěšci mohou proměnit jen na exokameny. (Partially tested with condition that pawns can be promoted only to fairy pieces) (added 19.10.2008, updated 17.2.2011) Problem was awarded with 1.H.M. (see The Problemist, January 2011, p.35, award fairies 2007), but here is published bad version. |
|
G6B - Joost de Heer F2516 The Problemist Nov.2006
|
1.g1LI b:a8LI(Sg8)+ 2.b:a1LI h:g8LI 3.e1LI g:h8LI(Lf8) 4.f1LI e:f8LI= Nový příklad G6B [8/8] se všemi 8 proměnami na liony. Alybadix tuto úlohu testoval 122 hodin 24 minut. (added 24.11.2006, updated 17.10.2007) |
|
G6C - Klaus Wenda 5679 feenschach 93/1989
|
1.d1G h:g8G(Lc8) 2.Gda4 d:c8G 3.a:b1G(Dd1) g:h8G(Dd8) 4.G:b3(Gb1) b:a8G(Ga1)= G6C [6/8] Alybadix tuto úlohu testoval 37 hodin 52 minut. (added 10.10.2007) |
|
G6D - Klaus Wenda 961 Phénix 13/1991
|
1.c:b1T(Lf1) c:d8T(Th8) 2.g:f1S g:h8S 3.h1D b:c8D(Sg8) 4.e1L f:g8L= cook 1.c:b1T(Lf1) c:d8T(Th8) 2.g1D g:h8S 3.Dh1 b:c8D(Sg8) 4.e1L f:g8L= G6D [8/8] Dva páry AUW. Je třeba poznamenat, že tato nekorektní úloha byla reprodukována dokonce v Albu FIDE 1989-91 (G82 str.563) (added 10.10.2007) |
|
G6E - Dezsö Elekes + Julius Toth + Lajos Szasz 2.-3.Pr. The Problemist 1927
|
1.Kb8 f:g8D 2.Kc7 d:c8T 3.K:d7+ e:d8L 4.Ke8 g:f8S= G6E [4/8] AUW se sekvencí jen bílých proměn. Skladba byla reprodukována např. v Ultimate Themes, T.R. Dawson 1938 (č.17 str.10) Alybadix testoval tuto úlohu 16 hodin 28 minut. (added 11.10.2007) |
|
G6F - Unto Heinonen Q0208 StrateGems 2007
|
1.Td8 e:d8L 2.Lf8 f:e8T 3.Da8 b:a8D 4.Kc8 g:f8S= G6F [4/8] AUW se sekvencí jen bílých proměn - druhý (a poslední) nalezený příklad na toto téma. (added 11.10.2007) |
|
G6G - Klaus Wenda 8442 feenschach 142/2001
|
1.c:b1L(Th1) f:e8L(Dd8) 2.h:g1T(Ta1) c:d8T 3.b:a1D e:f8D(Sb8) 4.d1S a:b8S= G6G [8/8], na doplnění ještě sekvence 8 ortodoxních proměn. AUW s korespondujícími proměnami černého a bílého. Úloha byla reprodukována ve StrateGems 38/2007 na str. 106 ovšem pouze s autorským řešením. Ale již ve feenschachu 149/2002 na str. 560 bylo publikováno, že úloha je nekorektní, např.1.c:b1L(Th1) Td1 2.Db8 a:b8S(Dd8) 3.La4 e:f8D 4.Lb3 c:d8T= (added 21.4.2007) |
|
G6H - Unto Heinonen 1.Pr. F2555 The Problemist May 2007
|
1.c1LI e8LI 2.b1LI h8LI 3.gh1LI cd8LI 4.e1LI ab8LI(Lf8) 5.f1LI gf8LI= G6H [10/10] Sekvenci dokonce 10 (!) proměn vykouzlil Unto Heinonen. Úloha je počítačem kompletně nepřezkušitelná. (added 17.10.2007) |
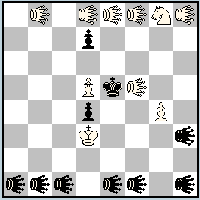
(patová pozice, stalemate position)
|
G6I - Norbert Geissler Die Schwalbe 117/1989
|
1.d1L f8D 2.b:c1T g:h8S= G6I [4/4] AUW (added 10.11.2007) |
|
G6J - Erich Bartel Problemas 58/1992
|
1.b1L f:g8D(Lc8) 2.g:h1T b:c8S= G6J [4/4] AUW (added 10.11.2007) |
|
G6K - Theodor Steudel Problemkiste 156/2004
|
1.a1L a8T 2.f:g1S f:e8D= G6K [4/4] AUW (added 10.11.2007) |
|
G7 - Norbert Geissler Problemkiste 1985
|
Sériovotahové úlohy1.c8G 2.g8G 3.e8G 4.b8G#Téma sekvenčních proměn vyznívá ještě působivěji v sériovotahových úlohách. Úloha G7 [4/4] přináší 4 sekvenční proměny. Bílý musí pokrýt pole a4 (cvrčkem z e8), b3 (cvrčkem z g8), c4 (cvrčkem z c8) a dát mat (cvrčkem z b8). Jde teď o jednoznačnost sekvence proměn. Matový tah musí být poslední a první tah je dán tím, že bílý král je v šachu od cvrčka a5 (přes pěšce c7). Okamžitou proměnou pěšce e7 by si bílý ale dal šach (od cvrčka h8), musí proto nejprve vstoupit do jeho linie proměnou na g8. |
|
G8 - Torsten Linss Problemkiste 1993
|
1.e8G 2.f8G 3.b8G 4.h8G# Také G8 [4/4] přináší 4 sekvenční proměny. I v této úloze je bílý král v šachu (od cvrčka c6), což určuje první tah. Ten však nemůže být proměnou pěšce b7, protože vstupem na b8 by si dal bílý šach (od cvrčka d8). V madrasi však pomůže proměna pěšce e7, kdy cvrček e8 nyní paralyzuje cvrčka c6 a ten už nedává šach. Motív paralyzace vidíme i v dalším tahu, kdy se promění pěšec f7 a tím (přes cvrčka e8) zparalyzuje cvrčka d8. Nyní je už možná proměna pěšce b7, protože cvrček d8 už nedává šach. Cvrček z b8 potom kryje pole b1 (a svým tahem navíc znemožnil černému cvrčku b2 odskok na b8). Matuje pěšec h7 po proměně na cvrčka. |
|
G9 - Norbert Geissler Jugendschach 1986
|
1.c8G 2.h:g8G 3.Gg6 4.g:h8G 5.f8G 6.a:b8G# Skladba G9 [5/6] má 5/6 proměn. |
|
G10 - Vaclav Kotesovec 6647 Problemkiste 164/2006
|
1.a8G 2.h:g8G 3.g:h8G 4.e:f8G 5.d8G 6.b:c8G= V úloze G10 [6/6] se mi nejprve podařilo zpracovat 6 sekvenčních proměn. |
|
G11 - Vaclav Kotesovec 5.H.M. 13068 Die Schwalbe 219/2006
|
1.d:c8G 2.b:a8G 3.a:b8G(Th8) 4.g:h8G 5.e:f8G(Gf1) 6.f:e8G 7.h:g8G(Dd8) 8.c:d8G= A k vysněným 8 proměnám mě přivedlo až podobné schéma v úloze G11 [8/8]. Sekvence 8 cvrčkových proměn v sériovotahové úloze, absolutní rekord! Cvrček a1 je paralyzován bílým cvrčkem h1, takže bílý král není v počáteční pozici v šachu. Není však možné hned brát černého cvrčka f8, protože po jeho přemístění na f1 by přestal být černý cvrček a1 paralyzován a dával by šach. Bílý proto musí nejprve změnit linii paralyzace a paralyzovat cvrčka a1 bílým cvrčkem z h8. Potom už je možné braní čCf8, protože po jeho přemístění na f1 už nevadí, že byla tímto přerušena linie bCh1 k čCa1. Tento specifický madrasi motív umožnil na sebe jednoznačně navázat sekvence bílých proměn. C+, Alybadix testoval tuto úlohu přes 340 hodin, AMD64 / 4200 MHz. Tested over 340 hours! Komentáře řešitelů: "Alle BB wandeln sich in GG um und lähmen" (RSch). "Die Grashüpfer-Umwandlung liegt auf der Hand. Die Kompositions-Leistung liegt in der genauen Bestimmung der Reihenfolge" (WW). "Achtfache G-UW. Leicht zu lösen, dafür aber wohl ungleich schwieriger zu komponieren, da Begründungen für die Reihenfolge gebraucht werden" (SB). "Das löst sich viel schneller, als es auf den ersten Blick aussieht, wenn man annimmt, dass sich alle wBB in GG umwandeln (und der Erfolg gibt Recht). Dann stellt man fest, dass die a-/b-Bauern über Kreuz schlagen müssen, ebenso die c-/d-, e-/f- und g-/h-Bauern. Als erster Zug ist aber nur einer dieser Züge möglich, im zweiten dann auch nur einer, und so ist es bei jedem folgenden. So läuft die Lösung wie ein VW-Käfer - pardon: wie ein Uhrwerk - ab. Wegen Circe werden die leeren Felder der 8. Reihe rechtzeitig besetzt; wegen Madrasi sind am Ende alle sGG zugunfähig (und manche Züge nicht früher möglich). Raffinierte Konstruktion" (BS). "Eine achtfache G-Umwandlung ist - trotz des riesigen Materialaufwands - immer noch ein Kraftakt bei der Konstruktion und sehenswert" (KHS). Dále je v Die Schwalbe 222/2006 na str.660 uvedena pro srovnání úloha G14, ve které je ale "jen" 7 proměn z celkem 16 tahů spojeno s proměnou na cvrčky, takže téma tohoto článku (aby byly všechny tahy s proměnou) nesplňuje. Je připojen komentář: "Zum Vergleich eine Aufgabe mit siebenfacher G-Umwandlung, ohne Märchenbedingungen, aber mit doppelt so vielen Einzelzügen." |
|
G11A - Vaclav Kotesovec 5.H.M. F2487 The Problemist 7/2006
|
1.d:c8S 2.b:a8L 3.a:b8S(Th8) 4.g:h8D 5.e:f8T(Gf1) 6.f:e8G 7.h:g8G(Dd8) 8.c:d8L= Na doplnění uvádím ještě jednu úlohu, kde podobné schéma (obsahující proměněné kameny) umožnilo zpracovat sekvenci proměn 8 bílých pěšců obsahující i tzv. superAUW (všeproměnu včetně cvrčka). Alybadix testoval tuto úlohu 12 hodin 39 minut. Comments of solvers: "Brilliant forcing of order of 8 promotions this time, avoiding potential self-checks from Ra8, Bc8, Qa1 and checks from Ge8, Gg8. BK ends up mirror-stalemated in Madrasi crossfire. Not a superfluous unit on the board. Lovely." (CCL), "As expected all wPs promote but cleverly done to force move order and choice of promotions." (CCF), "Difficult problem with promotion." (RL), "I thought it not too difficult to solve but a satisfying knot to unravel." (SE) Judge Hans Gruber (The Problemist, September 2011, p.214): "8 moves - 8 promotions! Of course such a task requires many captures, but rebirths and paralyses are integrated in an elaborated manner." Úloha byla též reprodukována v "Pat a Mat" 55/2006 na str.404. (added 26.7.2006, updated 22.11.2011) |
|
G12 - Joost de Heer F605 Probleemblad 6-2006
|
1.d1LI 2.a1LI 3.f1LI 4.g1LI d8LI= Nový příklad G12 [5,5] se 4 proměnami černého, doplněný ještě pátou proměnou bílého. (added 30.12.2006) |
|
G13 - Unto Heinonen F606 Probleemblad 6/2006
|
1.c:d8D(Dd1) 2.d8S 3.a:b8S(Sg1) 4.b8L 5.e:f8T(Ta1) 6.f8T 7.h:g8L(Lf1) 8.g8LI= Nový příklad G13 [8,8] s originální sekvencí 8 různých proměn. Redaktor v Probleembladu píše, že nebyl schopen úlohu kompletně otestovat. Zkusil jsem ji testovat Alybadixem a zjistil jsem, že úloha je korektní za předpokladu, že jde o Anticirce Cheylan. Pokud by šlo o Anticirce Calvet, měla by úloha vedlejší řešení 1.c8L 2.e:d8D(Dd1) 3.d8L 4.L:e6(Lf1) 5.Lc7 6.g:f8S(Sg1) 7.f8T 8.h:g8LI(LIg8)= V případě, že jde o Anticirce Cheylan, braní na circe poli g8 v matícím tahu není možné. Alybadix ji testoval jako Calvet přes 60 hodin a jako Cheylan 33 hodin. (added 6.1.2007, updated 10.1.2007 and 25.1.2007) |
 (pozice před patovým tahem) |
Nemohl jsem pochopit, čím je kryté f3, až mi to vysvětlil Ilkka Blom (autor Alybadixu): "bSe2 does NOT guard wSg1 since there is a piece on b8. Thus wSg1 can move to f3!"
Černý jezdec e2 nekryje g1 (a tedy ani neparalyzuje bílého jezdce g1), protože je kámen na poli b8. Takže bílý jezdec g1 může táhnout na f3! Když se na to podíváme obráceně, tak bílý jezdec g1 může brát černého jezdce e2, protože circe pole b1, kam by se po braní bílý jezdec přemístil, je volné. Černý jezdec e2 je proto v Madrasi paralyzován, ale bílý jezdec g1 ne! Je neuvěřitelné, že i v případě dvou jezdců, může být paralyzace jednostranná (jako třeba u cvrčků) ! Anticirce je příšerné... Je vidět, že z anticirce má "zamotanou hlavu" i program Popeye, který řešení nenajde (a to ani v jednom z případů Calvet / Cheylan) Úlohu správně řeší kromě Alybadixu i WinChloe (řešeno jako =1 před posledním tahem). Popeye not found solution of this problem. Alybadix and WinChloe solved correctly. |
|
G13A - Unto Heinonen F606v Probleemblad 2/2007 (page 56)
|
1.c:d8D(Dd1) 2.d8S 3.a:b8S(Sg1) 4.b8T 5.g:h8L(Lc1) 6.h8T 7.f:e8L(Lf1) 8.e8G= V této verzi si autor vystačil pouze se cvrčky. Alybadix ji testoval 7 hodin (AMD64 4200+). (added 21.7.2007) |
||||||
 (patová pozice, stalemate position) |
|
G14 - Klaus Wenda 2.Pr. StrateGems 1999
|
1.a8G 2.Ka7 3.Ga6 4.Ta8 5.e8G 6.Gc6 7.d8G 8.Gb6 9.c8G 10.Ggb8 11.g8G 12.g7 13.Gg6 14.g8G 15.h8G+ Gh7# G14 [7/16], jen 7 proměn z celkem 16 tahů je spojeno s proměnou na cvrčky, takže téma tohoto článku (aby byly všechny tahy s proměnou) nesplňuje. Přesto vhodná na doplnění celé problematiky. Úlohu nelze kompletně přezkoušet počítačem. |
|
G15 - Joost de Heer Sp.Comm. StrateGems 2004
|
1.c8T 2.hg8D 3.fe8S(Dd8) 4.ed8L= AUW G15 [4/4] (added 17.10.2007) |
|
G16 - Vaclav Kotesovec original (10.7.2007)
|
1.a:b8G 2.b:a8G 3.c:d8G 4.d:c8G 5.e:f8G 6.f:e8G 7.g:h8G 8.h:g8G= = G16 [8/8], jednoduchý, ale ne úplně triviální příklad. (Bez cvrčka h1 by měla úloha vedlejší již 7.tahem s proměnou na věž na poli h8.) (added 10.7.2007) |
|
G17 - Joost de Heer F2619 The Problemist 2008
|
1.f:e8N(Lc8) 2.b:c8N 3.d8N 4.g:h8N 5.h:g8N# G17 [5/5] - sekvence 5 proměn na tátoše. (added 28.3.2008) |