Hashing and pruning
(Vaclav Kotesovec, 18.4.2003)
Summary:
- For 8 halfmoves is solution of chess problems with hashing cca 12x faster than without hashing. This ratio is identical for all programs. (see Table 2)
- For each chess problem exist (in selected number of moves) maximal number of possible positions. These positions stored in hash memory. Size of memory is different for each program (see Table 3). Best is Alybadix, hash data are compressed.
- If program have less memory than necessary, must "pruning" and part of hash data must recomputing. If Alybadix or Popeye have 50% of necessary memory, are only 1.15x slower (this is good result!), but WinChloe is in this case 3x slower. (see Table 4)
- First 3 charts display relation between memory (in MB) and time of solution (in seconds) for each program.
- Next 3 charts (most important!) display relation between % of necessary memory and coefficient of slowing of programs (1.00 = time for infinite memory). This comparsion of programs is most objective, values are normalized.
- Next chart is zoom of previous chart (for program Popeye only) near zero (between 0%-2%). This situation correspond hundreds of "prunings" (for example if program have 500MB hash memory, but 20-30 GB necessary).
- Last 2 charts are memory ratio (these values are know for Alybadix only). Formula is "number of prunings" * "size of hash memory" / "necessary memory". Red graph is theoretical value for clearing of hash memory after this memory is full. For example for 50% is this value 2, for 20% is this value 5 and for 10% is 10. Area under red graph is "intelligence" of pruning alghoritmus.
- and relation between "number of prunings" and "coefficient of slowing".
O hashování je na mé stránce již jeden článek z roku 2000 Hashing, ve kterém je možno se seznámit s principy hashování a jejich aplikací v jednotlivých programech. Následující článek si klade laťku výše a snaží se programům "sáhnout až na dno". Cílem mých testů bylo zjistit, jak je který program dobrý v hashování, zejména jak se chová, když mu nestačí paměť RAM a musí část paměti uvolnit (tzv. "pruning") a pokračovat v řešení.
Pro testy jsem vybral následující úlohu:
Vaclav Kotesovec
3617 Phénix 91/2000
|
1.Vg3 Ce5 2.g5 Cf5 3.g4 Ch2 4.Jg5 Cf4#
1.Kh5 Cf8 2.g5 Ch4 3.Jf4 Cf6 4.Jg6 Cf5#
1.Kg5 Ch5 2.Kh6 Cf7 3.Vg5 Ch4 4.Jg7 Cf6#
|
Table 1
Samozřejmě první nás napadne porovnání programů podle časů, ale podobným testům bylo již věnováno hodně prostoru a výsledky nepovažuji až za tak zajímavé. Přesto sem patří tato tabulka (časy jsou pro 600 MHz):
| Program | metoda | čas [m:s] |
| Alybadix 2003 | brute force | 1:14 |
| Popeye 3.75 | brute force | 2:01 |
| WinChloe 1.49 | brute force Win | 2:16 |
| WinChloe 1.49 | brute force DOS | 3:08 |
| VKSach 8.7 | intelligent mode (h#4/RS) | 0:02 |
| VKSach 8.7 | brute force (h#4/S) | 3:24 |
(dále jsou uvedena pouze jména programů bez verzí)
Odtud vyplývá, že jednoznačně nejlepší čas má VKS v intelligent modu (ostatní programy neumí "intelligent mode" pro exokameny), ale tato tabulka je pouze orientační - článek je o něčem jiném.
Table 2
Zajímavější je, jaké zrychlení přináší samotné hashování. Zrychlení (acceleration) získáme jako poměr času řešení úlohy bez hashování (s nulovou pamětí) a času s pamětí tak velkou, že se do ní vejdou všechny možné pozice (a není tedy nutný pruning). Pro takovou paměť používejme dále pomocný termín "nekonečná paměť".
Je zajímavé, že toto zrychlení je u všech programů (Alybadix, Popeye, WinChloe) dost podobné (a je dáno délkou úlohy - čím bude mít úloha více tahů, tím bude zrychlení větší). Pro h#4 (8 půltahů) je zrychlení způsobené tím, že si program pamatuje to co už zkoumal, asi 11-13 násobné proti metodě kdyby zkoumal (procyklil) všechny možnosti.
For 8 halfmoves is solution of chess problems with hashing cca 12x faster than without hashing. This ratio is identical for all programs.
| Program | čas bez hashování | čas s hashováním (a nekonečnou pamětí) | zrychlení |
| Alybadix | 15:59 | 1:14 | 12.9 |
| Popeye | 22:19 | 2:01 | 11.1 |
| WinChloe | 27:01 | 2:16 | 11.9 |
| VKSach | 13:34 (h#4/) | 3:24 (h#4/S) | 3.99 |
(v případě WinChloe je použit "Windows mode", "DOS mode" hashování neumí)
Čas bez hashování signalizuje, jak dobrá jsou "střeva" jednotlivých programů při metodě "hrubé síly". Překvapivě dobrý výsledek má VKSACH, který však neumí hashování (v tabulce je použito srovnání s S-algoritmem).
Nabízí se ještě srovnání hashování s "S-algoritmem" (unique order of moves) ve VKSACHu (viz Algorithm descriptions - part of "Between chessboard and computer", V.Kotěšovec, 1996). Podle analýzy v "Mezi šachovnicí a počítačem" na str.284-286, je pro h#4 (délka úlohy z příkladu) řešení při použití "S-algoritmu" asi 4x rychlejší - což téměř dokonale odpovídá realitě (!), (při použití "S1-algoritmu" teoreticky asi 24x rychlejší, ten však nejde použit k 100% kontrole korektnosti. Pro srovnání h#4/S1 dává čas 0:45, což je zrychlení 18.08x)
Bylo by velmi zajímavé odvodit pro tuto funkci nějaký obecný vzorec, který by určoval zrychlení programu díky hashování v závislosti na počtu půltahů. Udělal jsem stejný pokus ještě i na dalších úlohách (pro h#5 je to už dost časově náročné) a celkové (průměrné) výsledky shrnuje tato tabulka:
| metoda | 6 půltahů (h#3) | 8 půltahů (h#4) | 10 půltahů (h#5) |
| hashování | 3x | 11-14x | 80-130x |
| S-algoritmus | 2x | 4x | 8x |
| S1-algoritmus | 5x | 24x | 120x |
Závěr: hashování je samozřejmě lepší než S-algoritmus (což je snadno odhadnutelné, protože zjišťování jednoznačnosti se v S-algoritmu provádí jen do úrovně 2), ale S-algoritmus nepotřebuje žádnou paměť!
Table 3
Dalším důležitým kritériem je porovnání skutečně potřebné paměti pro každý program (nejmenší takové paměti do níž se vejdou všechny možné pozice). V případě programu Popeye byla skutečně použitá paměť zjištěna průběžným sledováním pomocí "Windows task manageru" (pod Win2k/XP), zbývající 2 programy zobrazují tyto údaje automaticky. Počet možných pozic by měl být u všech programů zhruba stejný (mírné rozdíly mohou být způsobeny například (ne)ukládáním nemožných pozic nebo různými optimalizacemi)
For each chess problem exist (in selected number of moves) maximal number of possible positions. These positions stored in hash memory. Size of memory is different for each program. Best is Alybadix, hash data are compressed.
| Program | potřebná paměť | počet možných pozic | přibližný počet bytů na 1 pozici (pro 7 kamenů) |
| Alybadix | 35 MB | 2643276 | ~ 13 |
| Popeye | 74 MB | nejde zjistit | ~ 26 |
| WinChloe | 63 MB | 2963570 | ~ 21 |
Počet bytů na 1 pozici samozřejmě (lineárně) závisí na celkovém počtu kamenů.
Jednoznačný závěr z těchto údajů je ten, že nejúspornější je (při identických podmínkách) Alybadix, který díky kompresi hashovaných dat potřebuje zhruba jen polovinu paměti ve srovnání s oběma zbývajícími programy.
Následující 3 grafy určují spotřebovaný čas v závislosti na dostupné paměti (naštěstí je tato hodnota ve všech programech nastavitelná). Podstatné body v těchto grafech nastávají v okamžiku, kdy paměť již zcela postačuje a větší pamětí už nic nezískáme (čas bude stejný).
Zajímavé jsou "časové skoky" u programu Popeye v oblasti mezi 3-13 MB, ne nejde o chybu, celou tuto oblast jsem pro jistotu testoval dvakrát. Zajímavá závislost!
Relation between memory (in MB) and time of solution (in seconds) for each program.
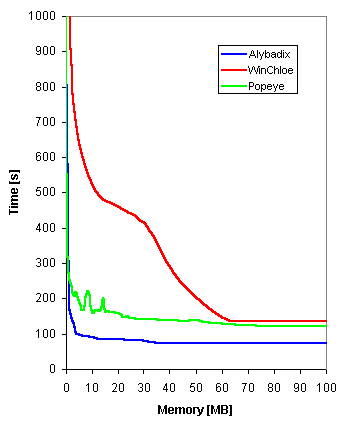
Při dosažení potřebné paměti pro tuto úlohu (35MB pro Alybadix, 74MB pro Popeye, 63 MB pro WinChloe) zůstává čas konstantní.
Table 4
Předchozí srovnání bylo sice zajímavé, ale šlo o kombinaci síly každého z programů s hashováním. Snažil jsem se však vymyslet způsob, jak objektivně porovnat pouze hashování ve všech programech. To lze provést tak, že hodnoty v předchozích grafech "znormalizujeme", přičemž 100% bude vždy odpovídat právě nejmenší potřebné paměti (je jiná pro každý program). K tomuto relativnímu zobrazení podle paměti RAM vypočteme "koeficient zpomalení" relativně podle odpovídajícího času pro 100% potřebné paměti. Pokud například Alybadixu stačí 35MB RAM, bude 100% 35MB, 50% 17.5MB atd. Analogicky čas pro 35MB (nebo obecně pro nekonečnou paměť) získá koeficient 1.00 a ostatní časy budou relativní k tomuto času.
Nyní se dostáváme k nejzásadnější tabulce, která určuje, jak efektivní je "pruning" u jednotlivých programů. Poznáme to podle času řešení, pokud má program například jen 50% potřebné paměti. Zatímco Alybadix i Popeye jsou v tomto případě pouze o 15 procent pomalejší, WinChloe jsou pomalejší téměř 3x. Nejlépe tedy vyznívá toto srovnání pro Alybadix a Popeye. WinChloe potřebují na to, aby byly stejně rychlé jako Alybadix nebo Popeye, mnohem více paměti.
If program have less memory than necessary, must "pruning" and part of hash data must recomputing. If Alybadix or Popeye have 50% of necessary memory, are only 1.15x slower (this is good result!), but WinChloe is in this case 3x slower.
| Program | zpomalení při 50% paměti | při 10% paměti |
| Alybadix | 1.15 | 1.5 |
| Popeye | 1.15 | 1.6 |
| WinChloe | 2.98 | 4.3 |
Dokonalý přehled získáme z těchto stěžejních grafů:
Relation between % of necessary memory and coefficient of slowing of programs (1.00 = time for infinite memory). This comparsion of programs is most objective, values are normalized.
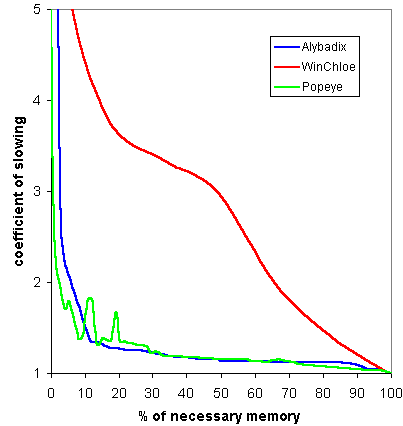
Tento graf bude velmi podobný pro všechny úlohy. Alybadix i Popeye dosahují dobrých výsledků i s menší pamětí. Zvlnění grafu pro Popeye je záhadou.
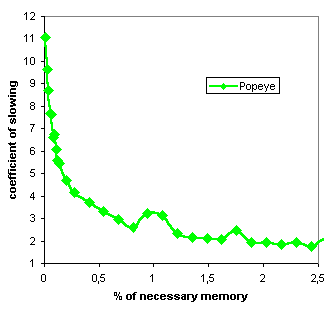
Ještě je zajímavý zoom tohoto grafu v okolí nuly (zoom "near zero"). Přesné měření bylo možné pouze pro program Popeye (v případě Alybadixu by ale byly výsledky podobné, jen průběh grafu by byl hladký), který umožňuje jemnější nastavení hashovací paměti (pomocí -maxmem) přesně v kB. Smyslem experimentu bylo však simulovat identické chování programů v situaci, kdy mají sice k dipozici paměť v řádu stovek MB, ale potřebná paměť se pohybuje v řádu desítek GB. Tato část grafu odpovídá právě této situaci, kdy program dělá stovky "pruningů". Podle chování grafu v okolí nuly je také možný lepší odhad celkového času řešení časově velmi náročných úloh.
Při porovnání chování grafu v okolí 0 (mezi 0%-2%) s dřívějšími výsledky řešení některých úloh Alybadixem, které vyžadovaly desítky hodin strojového času, se potvrdil stejný tvar grafu v obou případech.
Zoom of previous chart (for program Popeye only) near zero (between 0%-2%). This situation correspond hundreds of "prunings" (for example if program have 500MB hash memory, but 20-30 GB necessary).
Další graf představuje následující vzorec:
"počet pruningů" * "velikost hashovací paměti" / "potřebná paměť"
Počet pruningů je znám pouze pro Alybadix. Tento program v případě zaplnění hashovací paměti ponechá 25% hodnot (těch jejichž nový výpočet by byl nejnáročnější - otázka je samozřejmě jak je tato selekce pozic dobrá...). Zbylé tři čtvrtiny uvolní pro nová data. Stejná situace se pak opakuje i při dalším pruningu atd.
Pokud například při paměti 1 MB je potřeba u této úlohy 151 pruningů, neznamená to ovšem, že potřebná paměť bude 151 MB. Řadu hodnot je totiž třeba přepočítávat vícekrát. Pro 2 MB je už nutných jen 61 pruningů, pro 3 MB jen 34, pro 10 MB jen 7 atd. Potřebná paměť byla v tomto případě 35 MB. Obráceným postupem lze podle tohoto grafu z dílčích hodnot odhadnout velikost potřebné paměti.
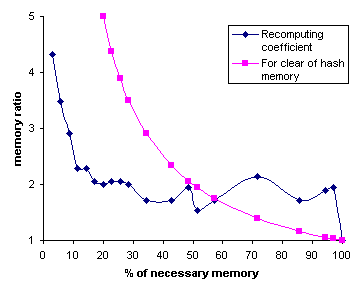
Graf přibližně určuje, kolikrát je nutno (v důsledku nedostatku paměti) přepočítávat stejné hodnoty v závislosti na relativní velikosti hashovací paměti. Hodnota 2 pro 50% je celkem očekávaná. Velmi dobré jsou hodnoty v intervalu 10%-50% (například hodnota stále kolem 2 pro 20% je vynikající a lepší než teoretická hodnota 5 odpovídající nulování hashovací paměti při jejím zaplnění). Hodnoty mezi 0%-10% jsou už trochu horší, ale stále relativně dobré.
Memory ratio (these values are know for Alybadix only). Formula is: "number of prunings" * "size of hash memory" / "necessary memory". Red graph is theoretical value for clearing of hash memory after this memory is full. For example for 50% is this value 2, for 20% is this value 5 and for 10% is 10. Area under red graph is "intelligence" of pruning alghoritmus (interesting are only values less than 50%).
Hodnoty na ose-x jsou opět normalizovány a představují procenta z potřebné paměti.
Relation between "number of prunings" and "coefficient of slowing".
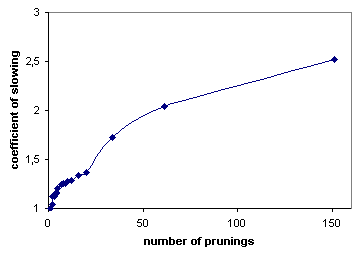
Tento graf zobrazuje zpomalení v závislosti na počtu pruningů v Alybaxidu.




